「3B1B-线性代数的本质」学习笔记

线性代数的本质
向量是什么
向量的三种理解
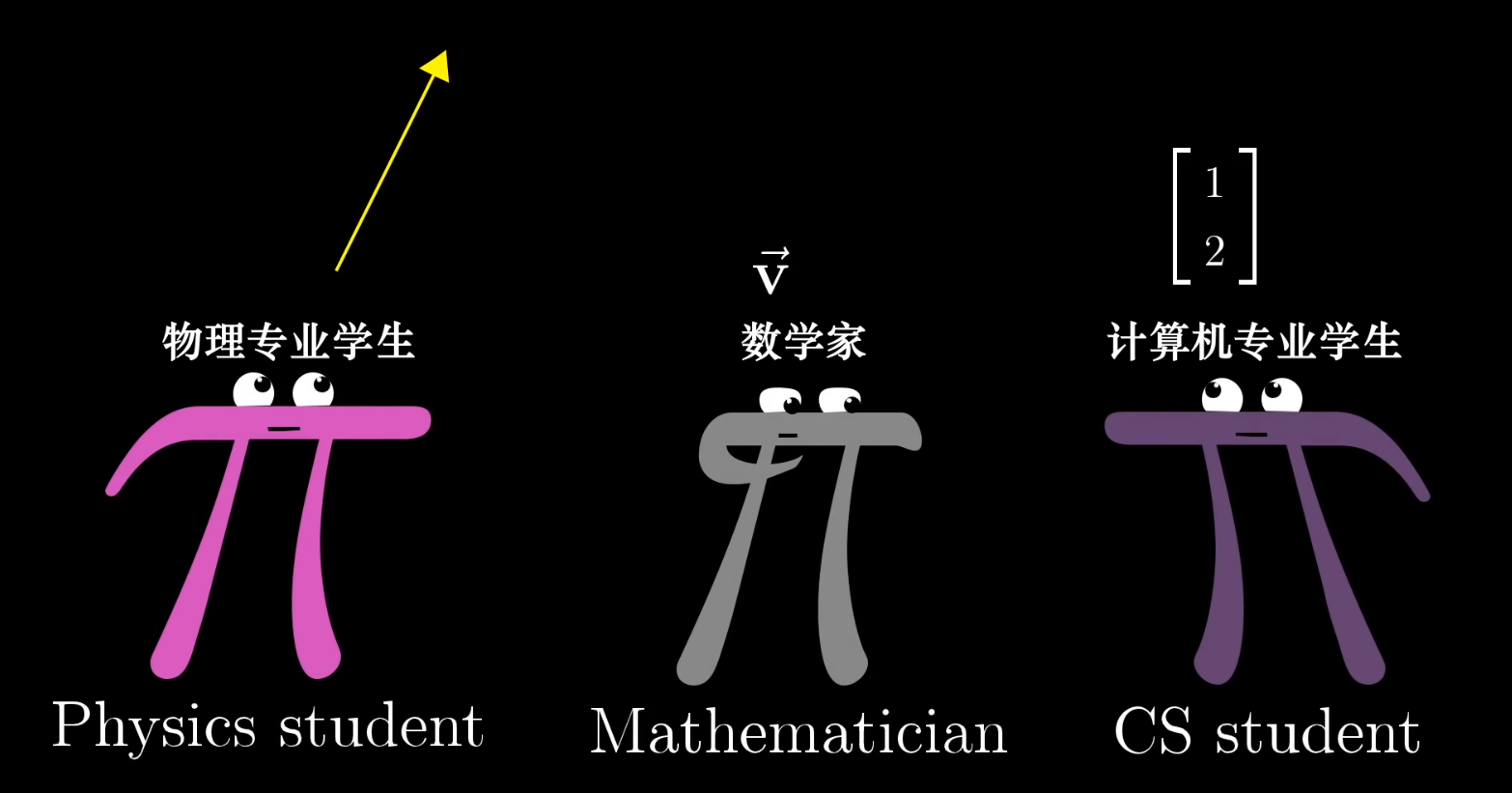
- 物理: 向量是空间中的箭头,决定一个向量的是它的长度与所指的方向
- 计算机: 向量是有序的数字列表
- 数学: A Vector can be anything! 只要保证两个向量相加/数乘有意义即可
线性代数中的向量
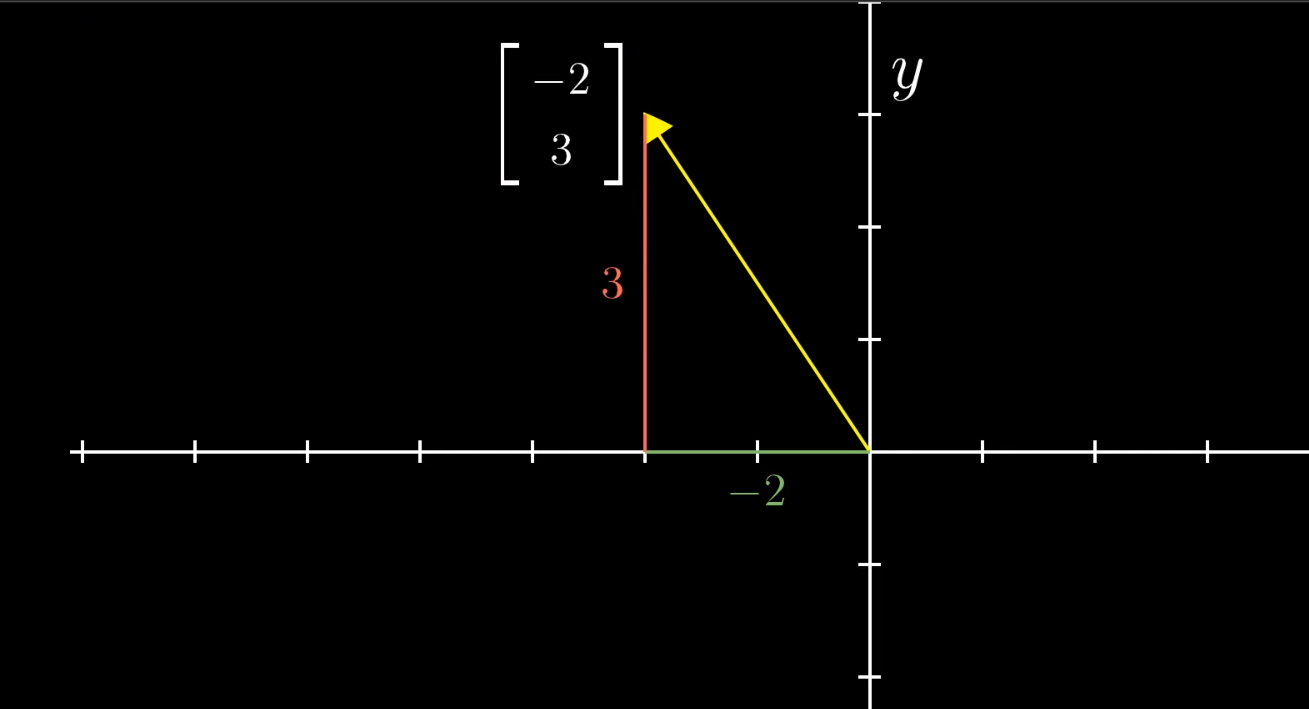
从几何直观的角度出发,线代中的向量是位于坐标系中且始终出发于原点的箭头,其坐标代表了其距离坐标轴的距离
(因为绝大部分情况下,向量的起点都是原点,所以有时我们也可以将向量看做坐标系中的一个点来进行理解)
向量的基本运算
- 加法: 三角形法则—描述了两个向量运动的叠加
- 数乘: 对于向量的拉伸、压缩、翻转
线性组合、张成空间与基向量
线性组合
两个数乘向量的和被称为这两个向量的线性组合
“线性”的一种理解: 在向量的组合中,如果固定其中一个标量,让另一个标量自由变化,所产生的向量的终点会描出一条直线
线性组合存在不同情况: 大部分情况下,v和w的线性组合可以到达二维空间中的任意点,而少部分情况下(共线/都是零向量)时,它们只能到达一条直线/原点
张成空间(span)
所有可以表示为给定向量线性组合的向量的集合被称为给定向量张成的空间
线性相关与线性无关
- 线性相关:
当我们有多个向量,并且可以移除其中的一个而不减小张成的空间,则这些向量“线性相关”
另一种表述,其中一个向量可以表示为其它向量的线性组合
- 线性相关:
如果所有的向量都给张成的空间增加了新的维度,则称这些向量“线性无关”
基向量
向量空间的一组基是张成该空间的一个线性无关的向量集
矩阵与线性变换
线性变换

“线性变换”中“变换”一词的本质便是函数,其接受输入并输出对应结果。
采用“变换”一词来描述,着重突出了其带有的“运动属性”,即并不是单纯的由a得b,而是由a运动到b,这对于向量有着非常好的几何直观
而线性代数中的变换,便是将向量空间中的所有点移动到另一个位置上

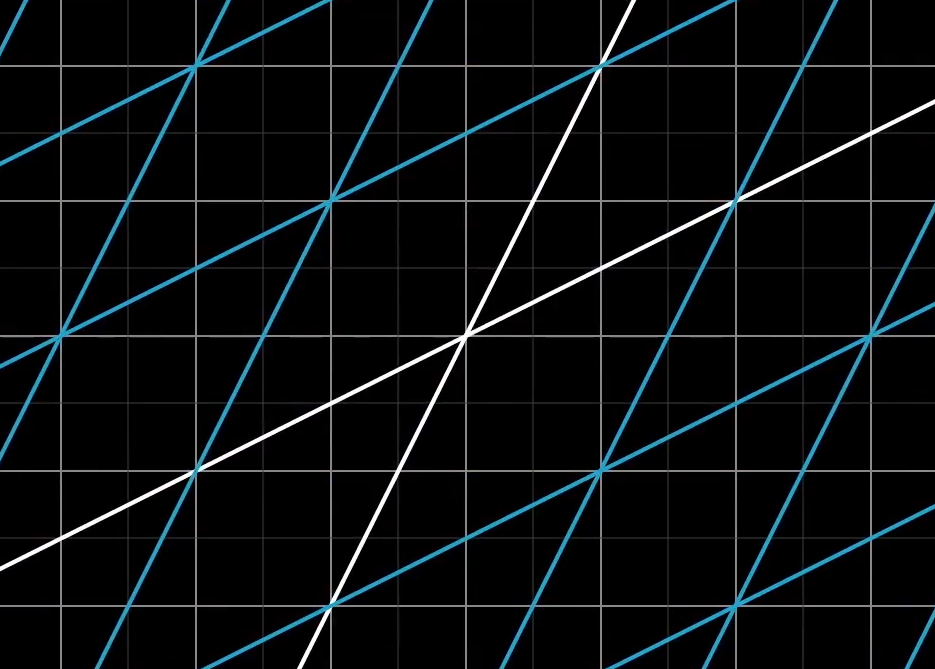
而线性变换便是一种特殊的变换,其有着两条性质:
- 直线在变换后仍为直线
- 原点不能移动
线性变换是让网格线保持平行且等距分布的变换,并保持原点不动
只需要记录变换前后的一组基向量,即可用其的线性组合描述空间中任意向量的对应变换
矩阵乘法的几何意义
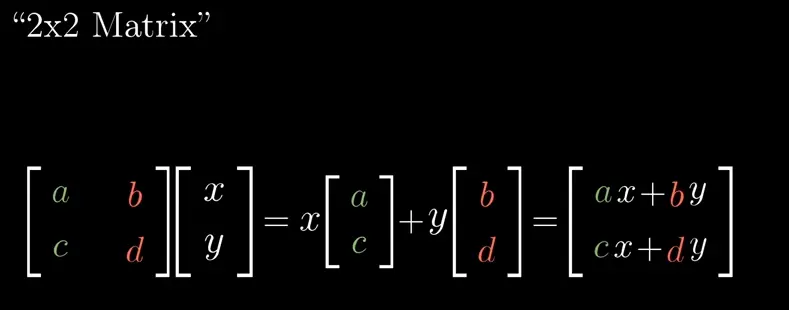
方阵的每一列都是一个基向量变换后的值,用方阵乘以(x,y)向量即可得(x,y)经过对应线性变换后的值
每当看到矩阵时,我们都可以把它理解为对空间的一种特定变换
矩阵乘法与线性变换的复合
线性变换可以复合,即多次独立的线性变换可以形成一个新的线性变换,这个变换被称为“复合变换”
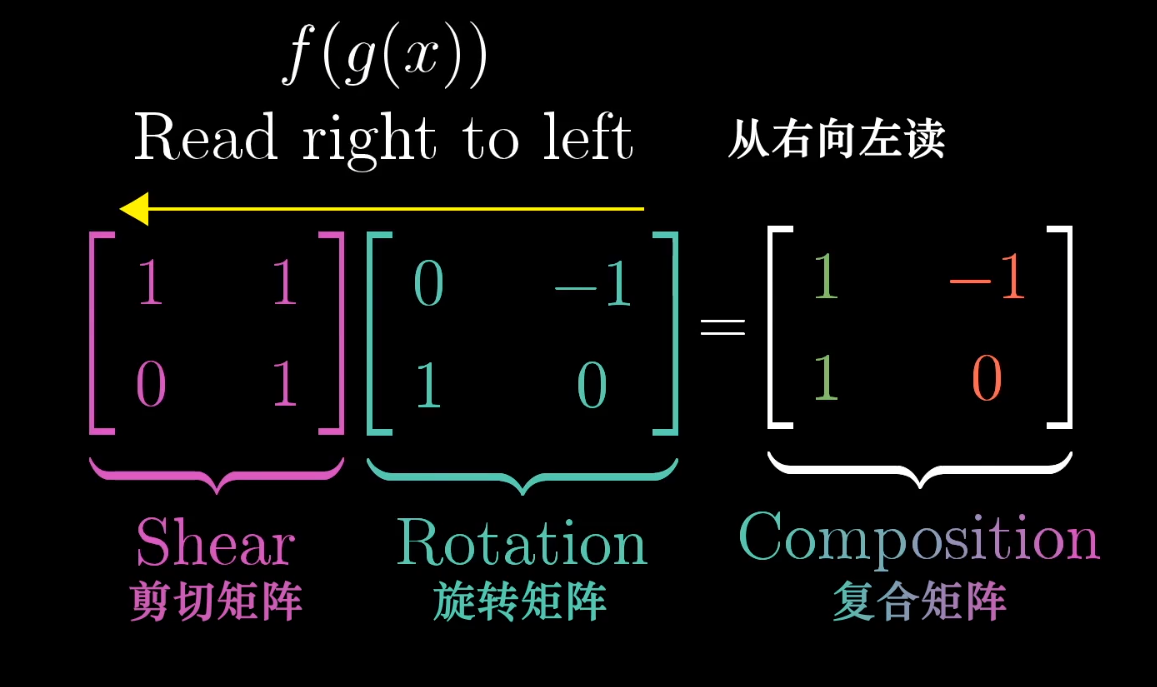
而复合变换的变换矩阵即为之前的独立线性变换矩阵的积,根据变换顺序,从右往左相乘
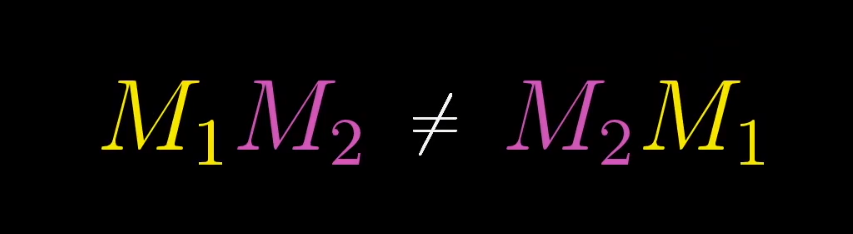
同时需要注意的是,矩阵乘法不具有交换律,反映到几何直观上,同样两次独立的线性变换,改变变换的先后顺序会使最后的复合变换改变
行列式
行列式的几何意义

线性变换改变空间面积的比例,成为变换的行列式

当行列式为0时,这意味着这次变换将一个平面压缩到了一条线/一个点上,将空间压缩到了更小的维度上
这对变换来说是一个非常有用重要的性质,这意味着这次变换是“线性相关”的
行列式的负数情况
根据行列式的几何意义,其代表空间改变的比例,但这无法解释为什么行列式存在负数
而这其实是由于空间的翻转导致的,有时变换会导致空间发生翻转,使得空间的定向(Orientation)发生改变,而行列式的负号表明了这点,此时行列式的绝对值仍然代表着空间的改变比例
三维空间的行列式的负数含义:由右手系变为左手系
逆矩阵、列空间与零空间
利用线性代数求解方程组
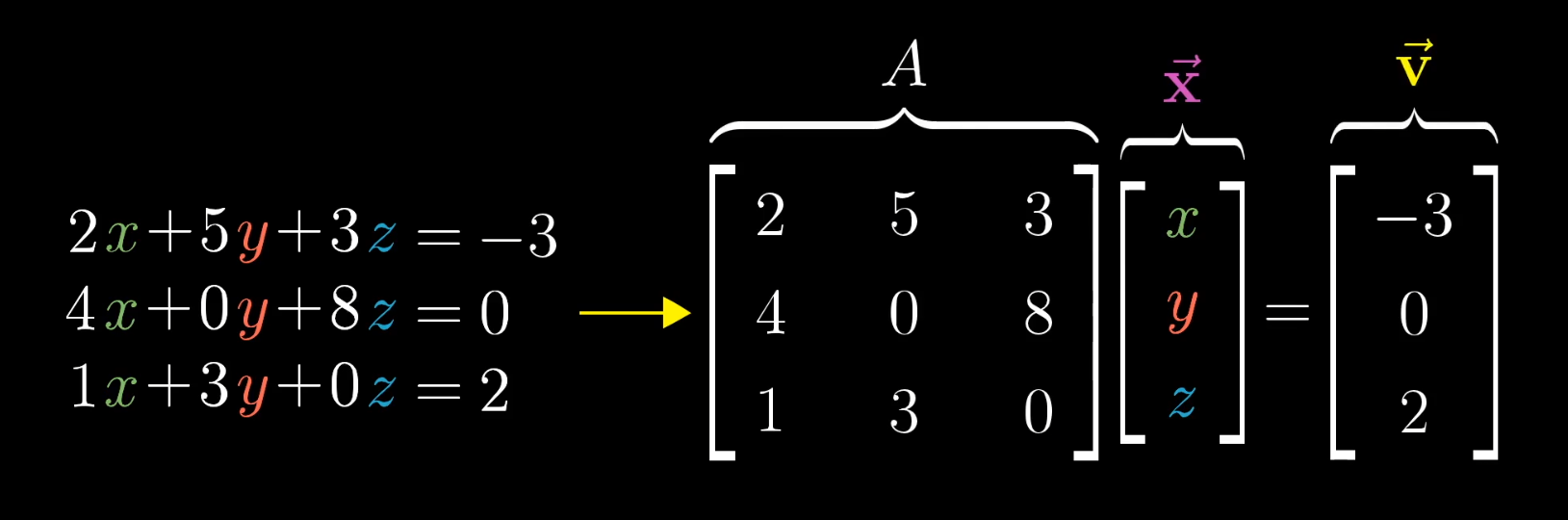
线性代数的一大应用便是其可以帮助我们求解线性方程组,我们可以将线性方程组抽象为一种将未知向量变为已知向量的特定的变换,赋予了方程组几何意义
- 当A变换行列式不为0时:
这代表着变换不会缩小空间的维度,意味着我们永远可以找到满足方程组的变换,之后只需要通过逆变换回溯变换就可以求出位置向量
- 当A变换行列式为0时:
这代表着变换会将空间压缩到更低的维度上,这种情况下逆变换将不存在,如果恰好目标向量正好仍在空间中,则可以求解,否则无解
对空间维度的压缩意味着会有多个输入对应一个输出
秩(Rank)

秩意味着变换后空间的维数
更准确的来说: 列空间的维数被称为秩
列空间
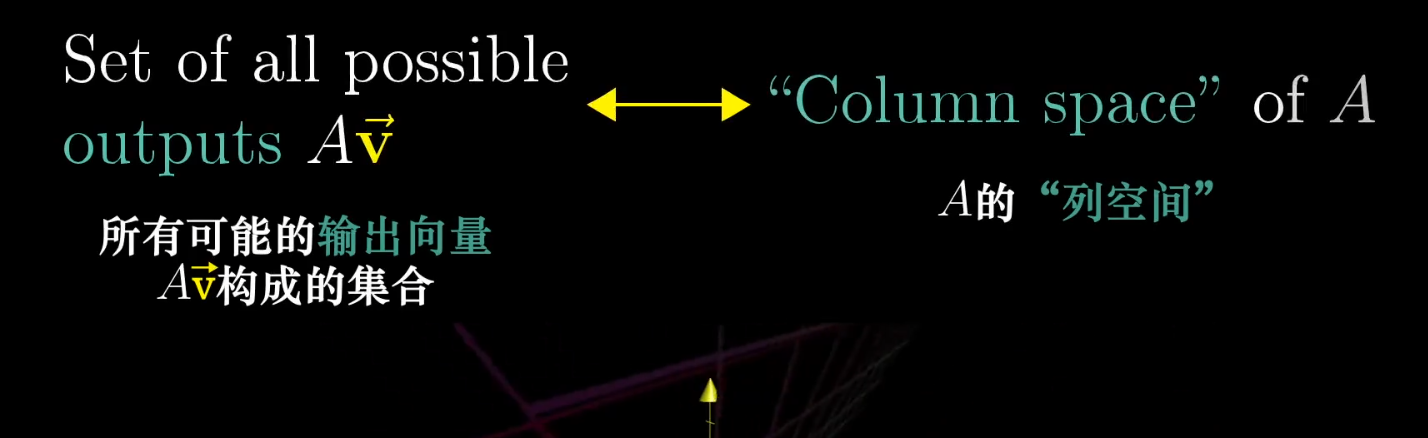
某一变换所有可能的输出向量的集合,被称为此向量的列空间
矩阵的列告诉你基向量变换后的位置,这些变换后的基向量张成的空间就是所有可能的变换结果
列空间就是矩阵的列所张成的空间
需要注意的是,因为线性变换规定原点不可变,故零向量一定会被包含在列空间中
零空间
一些向量在变换后会落在零向量/原点上,这些向量的集合被称为零空间
对于满秩的变换来说,零空间就是原点自身
而对于一个非满秩的变换来说,因为其对空间的压缩,会有某个面/某条线成为零空间
点积与对偶性
点积的标准解释
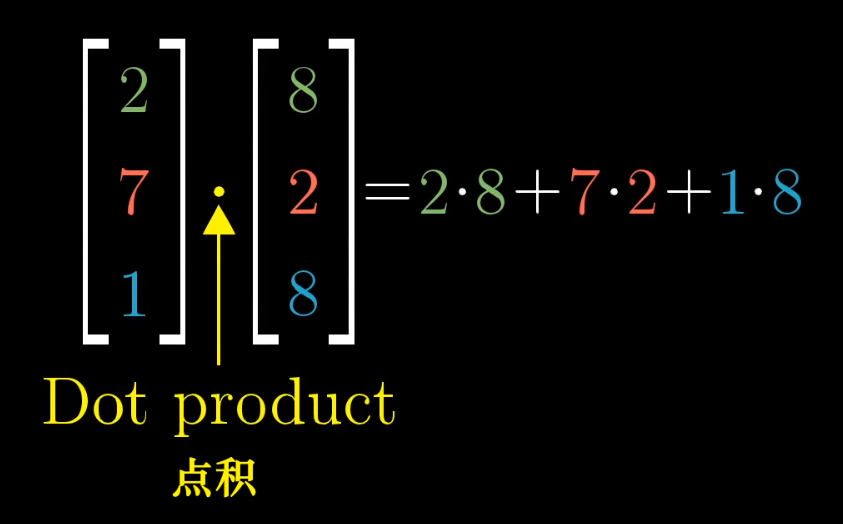
两个维数相同的向量,将对应坐标配对相乘后相加
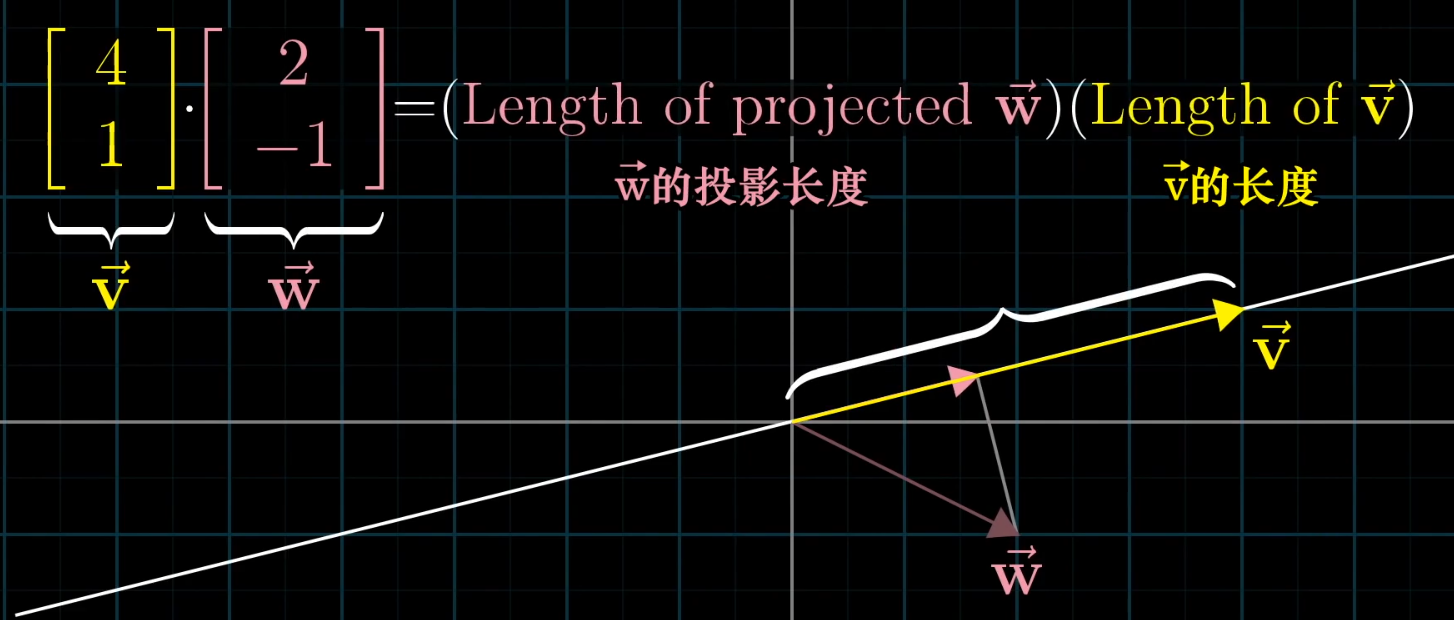
几何理解: 某一向量在另一向量上的投影长度与另一向量模长的乘积
线性代数视角中的点积
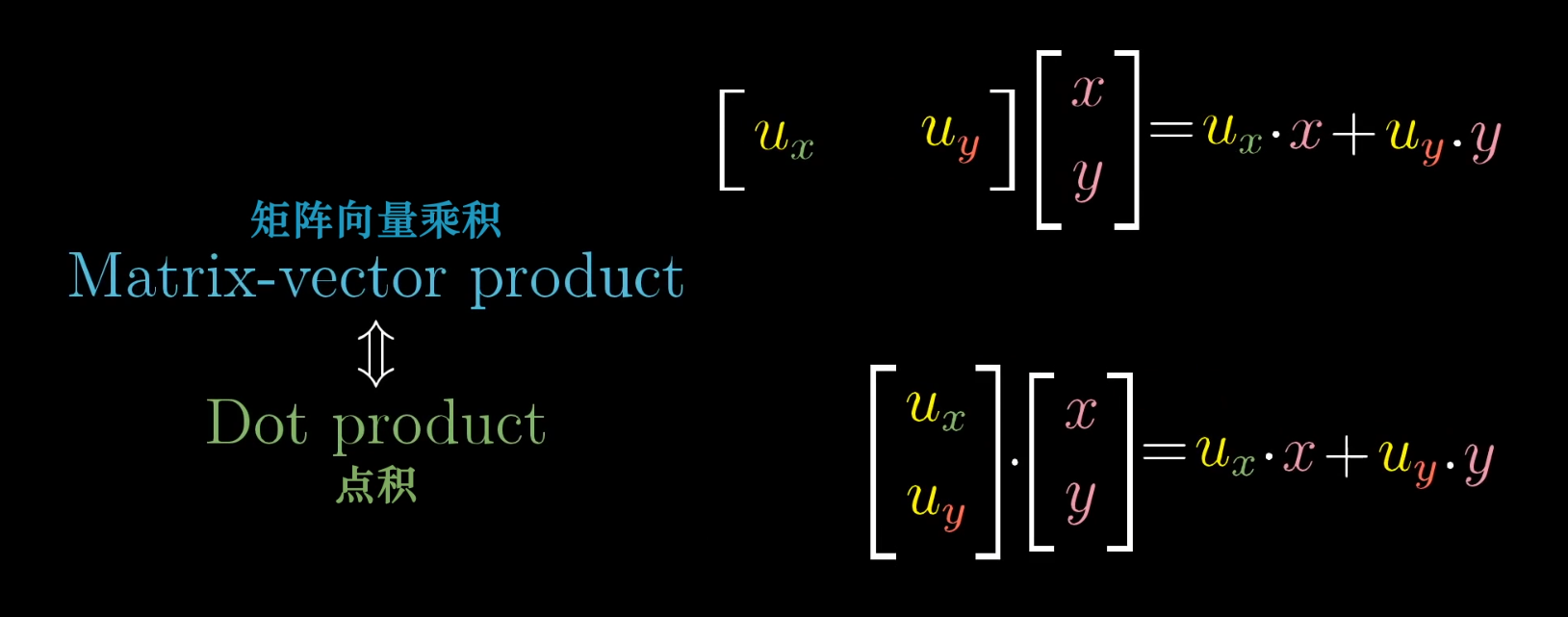
将点积中的某一向量看做一种由二维向一维的变换
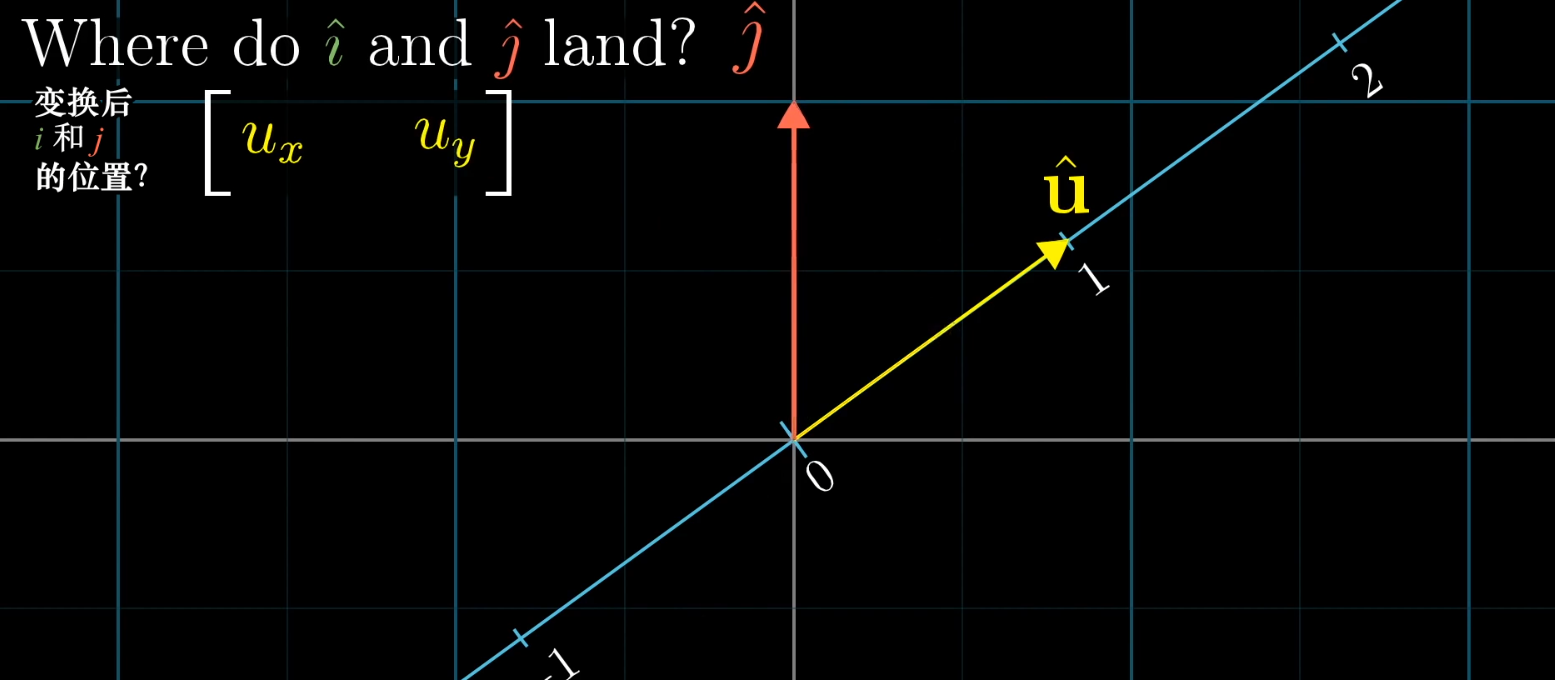
通过对称性,可以发现这种二维向一维的变换矩阵就是这一向量的x,y坐标,这太酷了!!!!!!!!!
叉积
叉积的标准解释
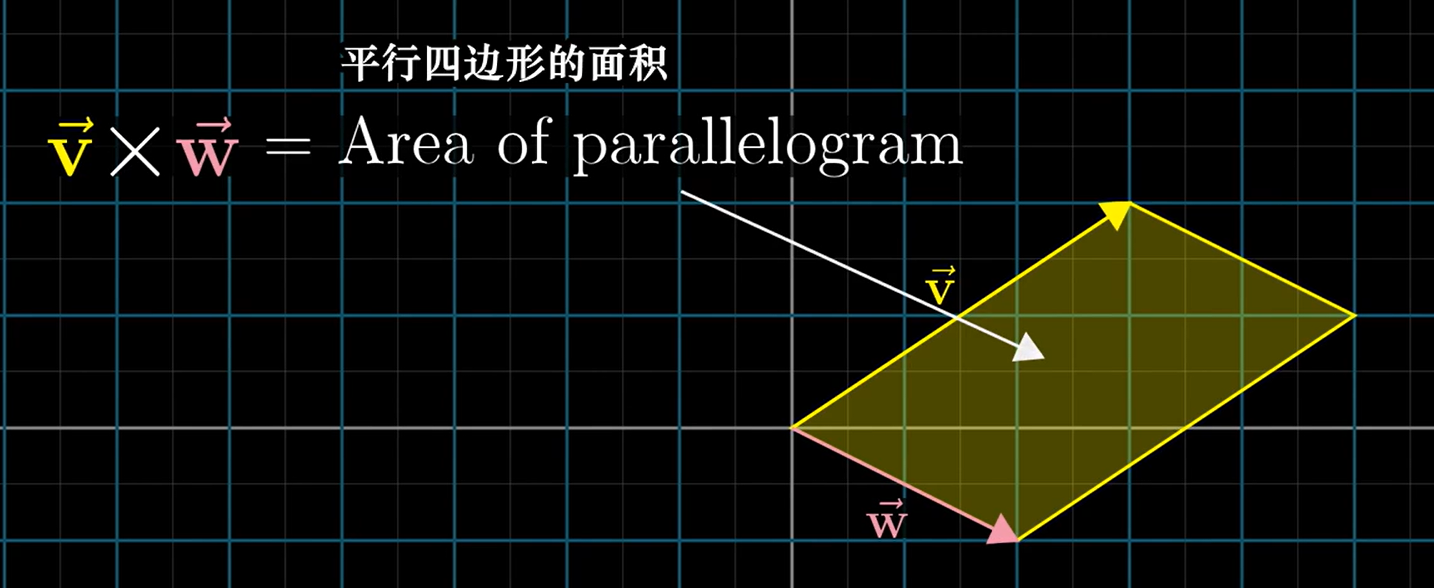
模长为两个向量通过平移形成的平行四边形的面积
方向为VW向量的相对位置
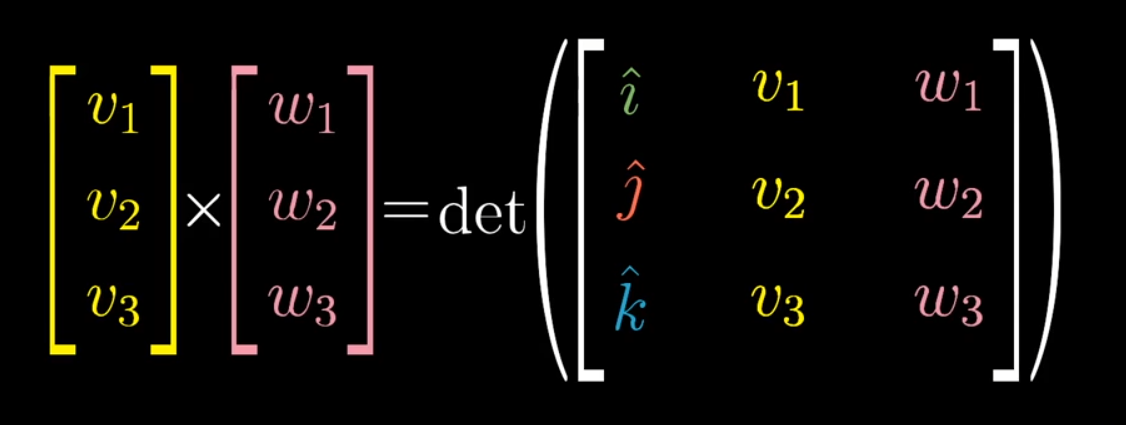
对于三维向量,其几何意义是依据右手系导出一个同时垂直于v、w的向量,且其模长为v、w形成的平行四边形的面积,计算公式如上
以线性代数的眼光看待叉积

基变换
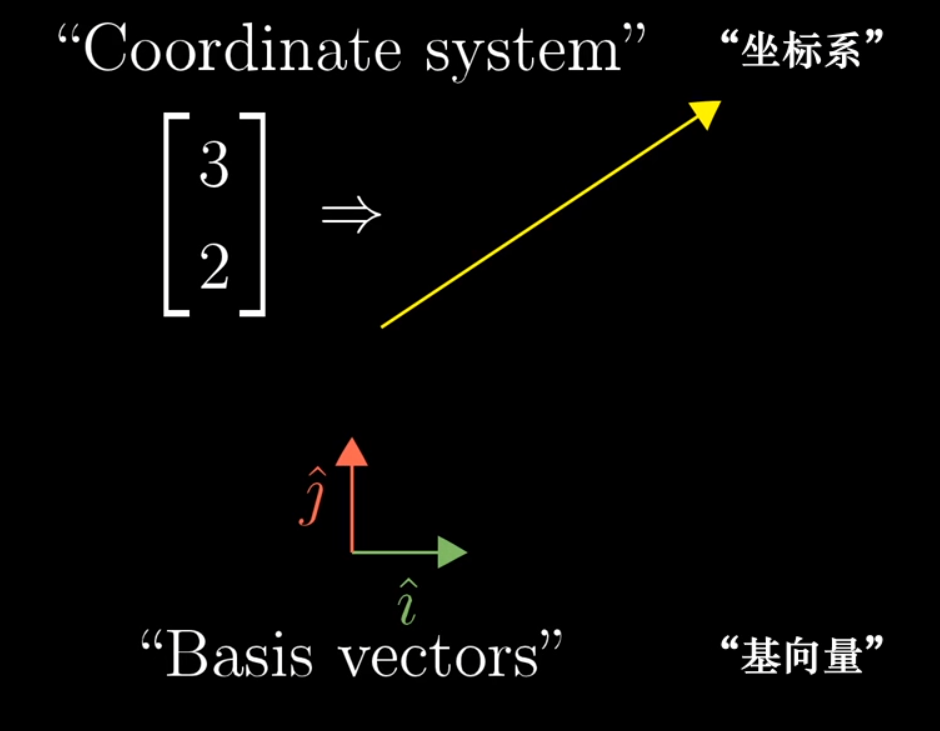
发生在向量与一组数之间的任意一种转化,都被称为一个坐标系
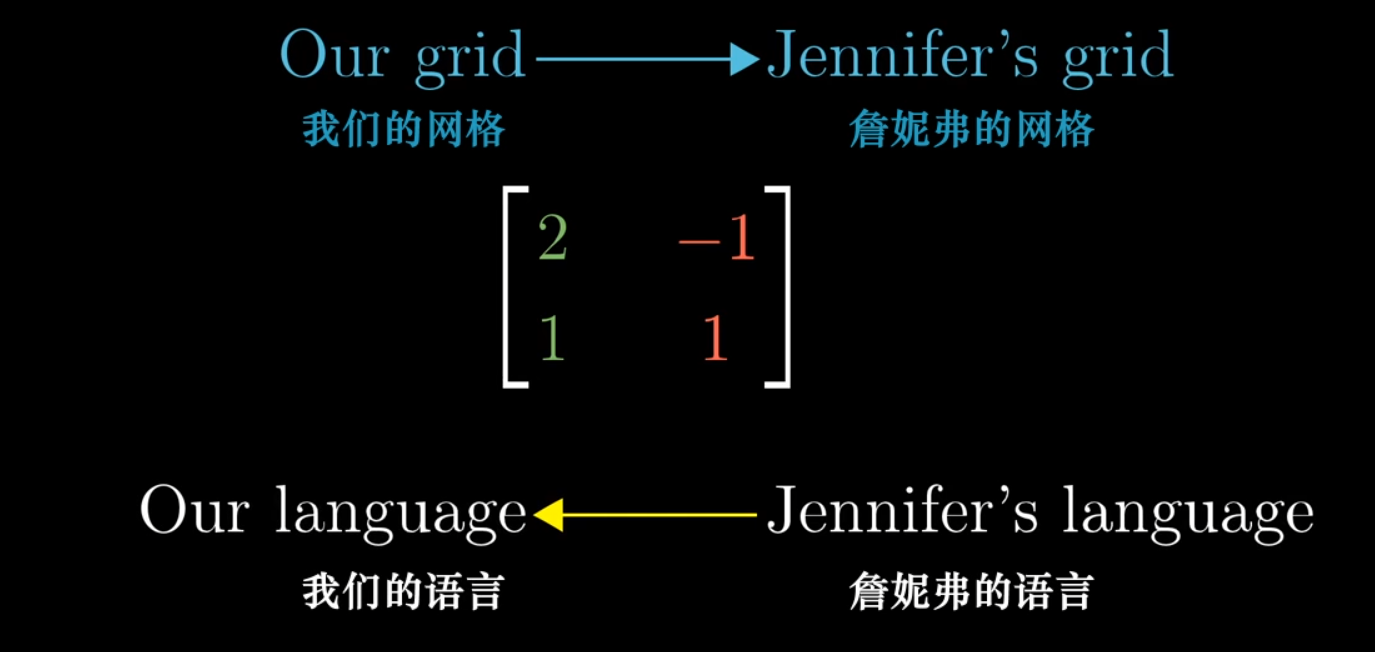
而坐标系的基向量规定了这种转化,采用不同的基向量,坐标系的映射关系便会发生改变
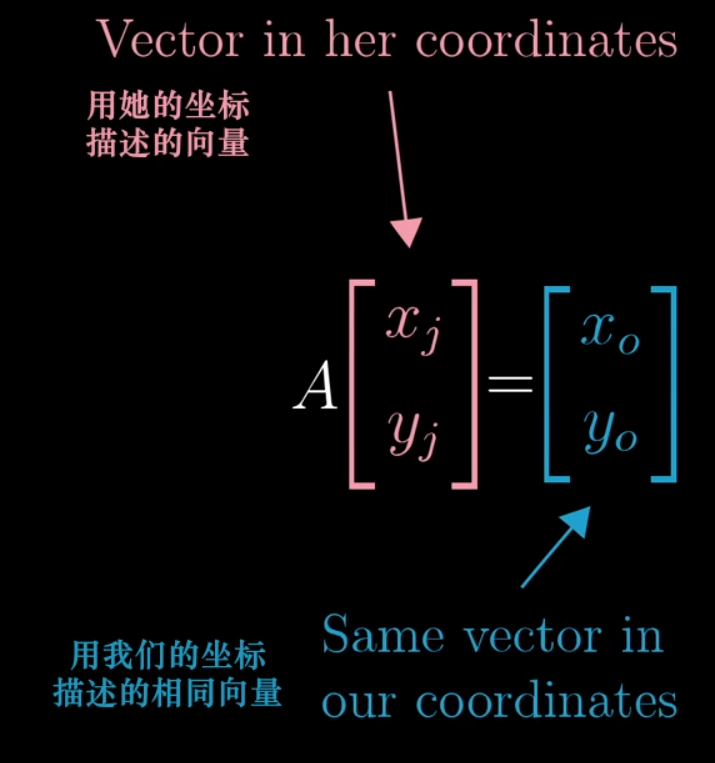
而通过变换矩阵可以实现基向量的变换
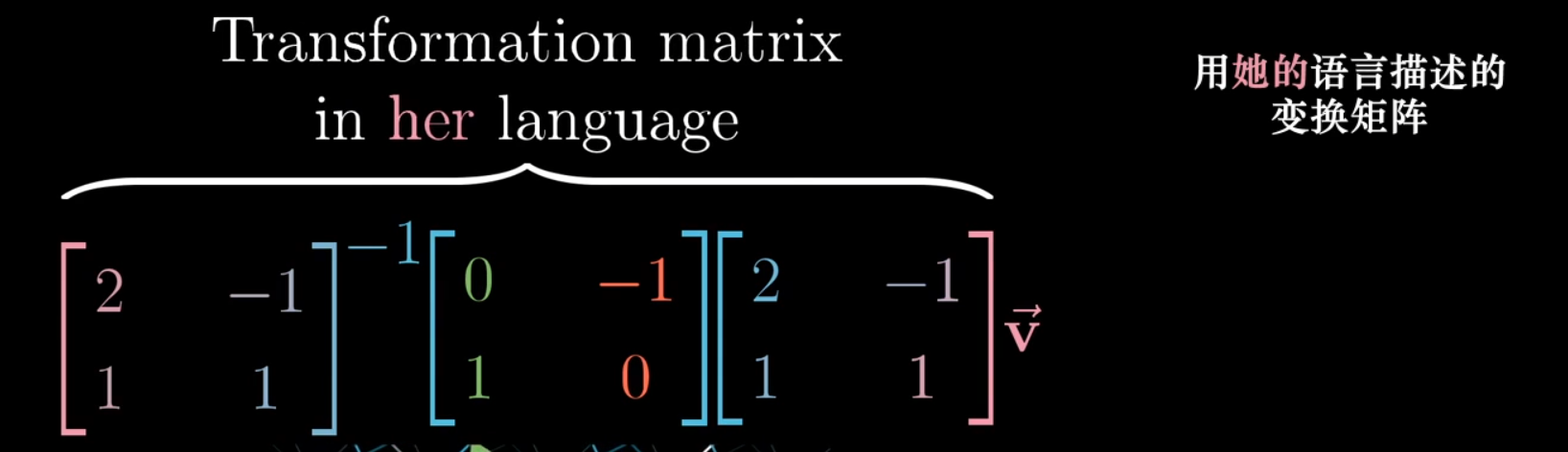
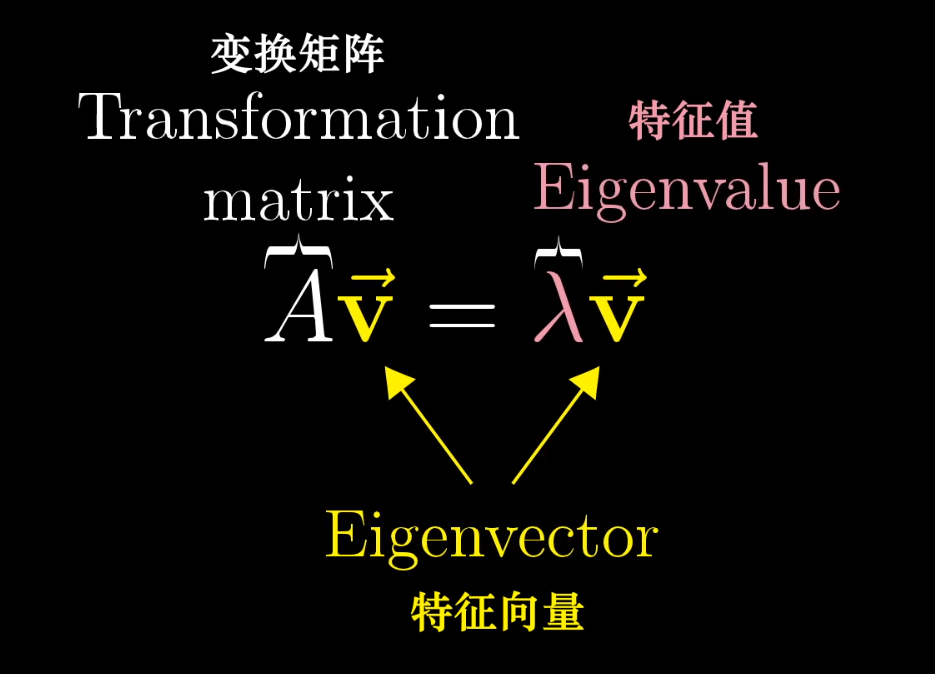
特征向量与特征值
定义

特征向量:在变换中张成方向保持不变的向量
特征值:特征向量被拉伸/压缩比例的系数
计算思想
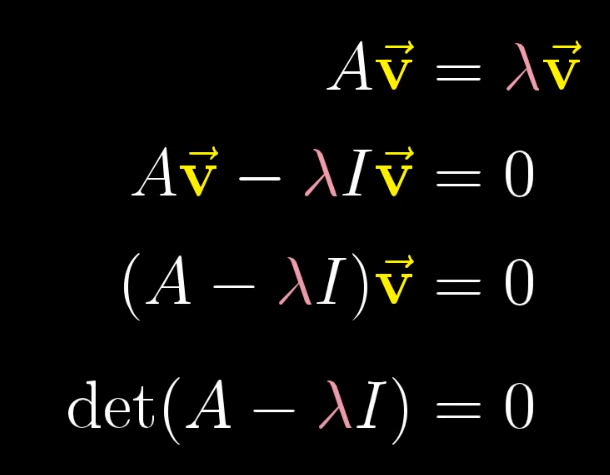
特征基
以特征向量为基向量会使许多计算变得简单
抽象向量空间
线性的严格定义
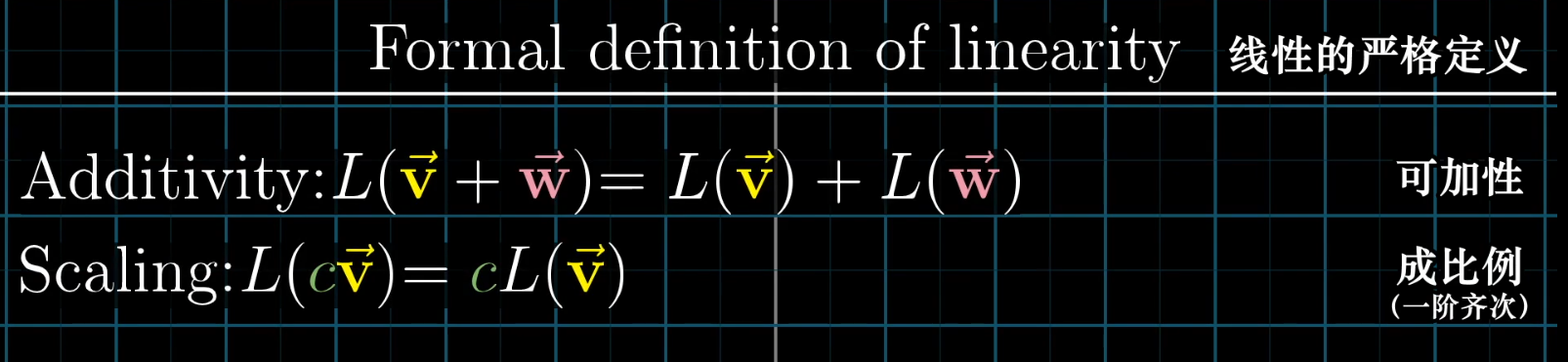
线性让一个线性变换可以通过它对基向量的作用来完全描述,这使得矩阵向量乘法成为可能
(求导就是一种线性运算)
函数与向量

向量空间
向量空间是抽象出来的无形概念,任何满足公理的东西都可以被称为向量空间,并应用向量的性质