基于柏林噪声的程序化地形生成

前言

随着图形学技术的高速发展，程序化生成技术（Procedural Generation）在游戏开发中的应用正在变得越来越广泛，从《我的世界》（Minecraft）、《文明》系列（Civilization）到各类类 Rogue 游戏，程序化生成技术展示了其巨大的潜力与无限的可能性，其很大程度上解放了生产力，让艺术家无需为庞杂繁琐的场景编辑而烦恼，也为游戏提供了无与伦比的重玩价值，让每一次“新游戏”都充满了惊喜。

在众多的程序化生成技术中，由 Ken Perlin 于 1983 年提出的柏林噪声算法（Perlin Noise）因其可以生成平滑、自然的噪声图像而备受青睐；其独特的平滑过渡的特性，使其在模拟自然现象、生成地形和纹理方面表现地尤为出色；在经久不衰的沙盒游戏《我的世界》的地图生成算法中就大量运用到了柏林噪声。

本文旨在以一个初学者的视角探索柏林噪声算法的原理、实现与其在程序化生成中的实际应用；笔者将使用 Unity 游戏引擎与 C# 语言实际实现具体的算法并将算法应用在实际的程序化生成中，如 2D Tilemap 的地图生成、 3D 类山地地形生成等；此外，为进一步提升程序化生成的效果，本文还将继续探讨一些柏林噪声的进阶应用与效果优化，如分形柏林噪声、渐进梯度算法、侵蚀算法等。同时，为了更加全面地了解程序化生成技术，本文还将简要介绍其它几种常见的算法，如 Simplex 噪声算法与 DLA 算法。

通过本文的探索，笔者旨在对程序化生成技术形成一个整体的认识，并了解其中的一些技术与算法的实现。

什么是柏林噪声

概述

在程序功能的实现中，我们常常会使用 rand() 函数来生成随机值来实现一些功能，但在这种简单的随机下，每次生成的值都有些太过“随机”了，其得到的结果往往参差不齐，而我们的世界并不是这样，山川河流都有其走势流向，当我们需要生成随机的地形或实现其他类似功能时，简单的随机往往不能满足我们的要求。而在计算机图形学中，噪声可以被描述为一种随机的信号；使用一些特定的噪声算法，我们便可以得到随机但过渡平缓的信号。

而柏林噪声（Perlin Noise）顾名思义也是噪声的一种，其特点在于其是一种可以产生连续平滑的可哈希的随机值的噪声生成算法，避免了传统噪声函数中常见的尖锐边界和不自然的过渡。其最早由 Ken Perlin 于 1983 年发明，最初被用于电影《电子世界争霸战》中的特效制作，并在 1985 年获得了奥斯卡科学技术奖。

柏林噪声的有着两点极其重要的特性：

梯度性：当其入参连续时，其返回的随机噪声值也连续
可哈希性：当入参相同时，返回值也相同

这两点给予了柏林噪声无与伦比的灵活性与泛用性。

原理

实现柏林噪声的核心思想实际并不复杂：通过插值实现平滑过渡的梯度；以下是具体的实现原理：

定义晶格并分配梯度

在某一维度的空间中，以一定固定间隔定义一个晶格，通过一定规则为每个晶格点分配一个随机梯度向量

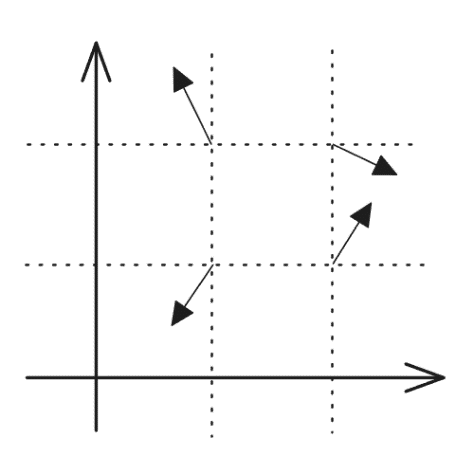
计算给定坐标点所处晶格

根据给定点可以得到其所处的晶格，在二维空间中即为4个相邻晶格点，可以得到晶格点到给定坐标点的向量

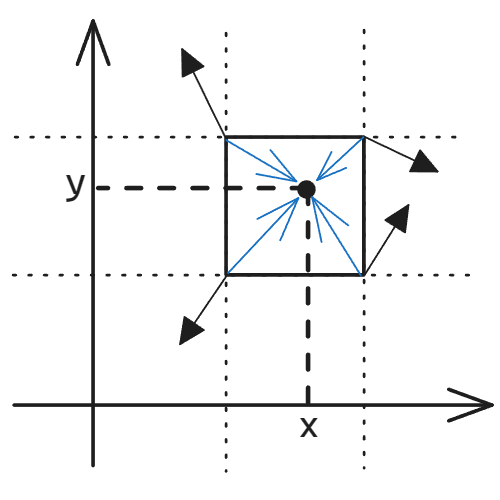
计算梯度值

对于每个晶格点，计算其梯度向量与步骤2得到向量的点积，这些点积值表示该点在每个晶格点方上的“影响”，此处称为“梯度值”

插值得到噪声值

使用插值函数，如二维平面中的双线性插值，对得到的梯度值进行插值，便可得到最终的噪声值

柏林噪声的算法实现

在上一章中，笔者简单介绍了柏林噪声的原理，这看上去并不难，但是在其实现上仍然有许多值得注意的点，笔者依据 Ken Perlin 在 SIGGRAPH 2002 上发表的论文《Improving Noise》在 Unity 中实现了柏林噪声算法的 C# 版本：

https://github.com/hmxsqaq/Unity-ProceduralMapGenerationPerlinNoise/blob/master/Assets/Scripts/PerlinNoise.cs

实际上 Unity 的 Mathf 库中提供了直接获取柏林噪声的方法，这里的实现是为了更好地理解算法，如果只是出于应用目的，直接使用库函数即可。

在笔者的版本中，笔者分别实现了二维空间与三维空间中的柏林噪声，二者的基本思路相似，以下将介绍 2D 柏林噪声算法的具体实现方式：

哈希序列

private static readonly List<int> Permutation256 = new(256)
{
    151, 160, 137, 91, 90, 15, 131, 13, 201, 95, 96, 53, 194, 233, 7, 225, 140, 36, 103, 30, 69, 142, 8, 99, 37,
    240, 21, 10, 23, 190, 6, 148, 247, 120, 234, 75, 0, 26, 197, 62, 94, 252, 219, 203, 117, 35, 11, 32, 57, 177,
    33, 88, 237, 149, 56, 87, 174, 20, 125, 136, 171, 168, 68, 175, 74, 165, 71, 134, 139, 48, 27, 166, 77, 146,
    158, 231, 83, 111, 229, 122, 60, 211, 133, 230, 220, 105, 92, 41, 55, 46, 245, 40, 244, 102, 143, 54, 65, 25,
    63, 161, 1, 216, 80, 73, 209, 76, 132, 187, 208, 89, 18, 169, 200, 196, 135, 130, 116, 188, 159, 86, 164, 100,
    109, 198, 173, 186, 3, 64, 52, 217, 226, 250, 124, 123, 5, 202, 38, 147, 118, 126, 255, 82, 85, 212, 207, 206,
    59, 227, 47, 16, 58, 17, 182, 189, 28, 42, 223, 183, 170, 213, 119, 248, 152, 2, 44, 154, 163, 70, 221, 153,
    101, 155, 167, 43, 172, 9, 129, 22, 39, 253, 19, 98, 108, 110, 79, 113, 224, 232, 178, 185, 112, 104, 218,
    246, 97, 228, 251, 34, 242, 193, 238, 210, 144, 12, 191, 179, 162, 241, 81, 51, 145, 235, 249, 14, 239, 107,
    49, 192, 214, 31, 181, 199, 106, 157, 184, 84, 204, 176, 115, 121, 50, 45, 127, 4, 150, 254, 138, 236, 205,
    93, 222, 114, 67, 29, 24, 72, 243, 141, 128, 195, 78, 66, 215, 61, 156, 180
};

private static readonly List<int> Permutation512 = new(512);

static PerlinNoise()
{
    Permutation512.AddRange(Permutation256);
    Permutation512.AddRange(Permutation256);
}

上述所示数组 Permutation256 与 Permutation512 为随机哈希序列，其中 Permutation256 中存储了随机顺序的 0 ~ 255，而 Permutation512 则为 256 数组的复制填充，目的是为了方便后续访问。

随机哈希数列提供了赋予晶格点随机梯度向量的能力，其决定了梯度向量的分配情况，理论上说这一哈希数列的元素顺序是可以随机分配的，而上述代码中手动定义的是 Ken Perlin 教授论文中定义的经典初始值。

需要注意的是上面说的“可以随机分配”是指可以每次初始化时重新随机，但是在同一轮柏林噪声的计算中，其不应该被改变，改变改数组会引起梯度向量的变化，这和柏林噪声希望的“伪随机”，即输入值相同、返回的随机值也应相同的理念背道而驰。

Lerp 与 Floor 函数

1
2
3

private static int Floor(float x) => x > 0 ? (int)x : (int)x - 1;

private static float Lerp(float a, float b, float t) => a + (b - a) * t;

Lerp 函数实现了线性插值，而 Floor 函数实现了向下取整，两个函数都为简单功能函数，它们也都在 Mathf 库中有对应实现，这里为了减少库依赖使用了自己实现的版本。

Fade 函数

1	private static float Fade(float x) => x * x * x * (x * (x * 6 - 15) + 10);

Fade 函数的实现也十分简单，但其起到的作用却非常重要。

在我们计算得到各个晶格点与给定点的梯度值后，我们需要根据给定点的相对位置将梯度值进行插值得到最后的噪声值，而如果我们仅仅使用最简单的线性插值，得到的结果并不会很平滑，特别是在晶格的交界处；而 Fade 函数实际起到了函数映射的功能，其表示的函数为： $f(x)=6x^5-15x^4+10x^3$ ，其图像如下所示：

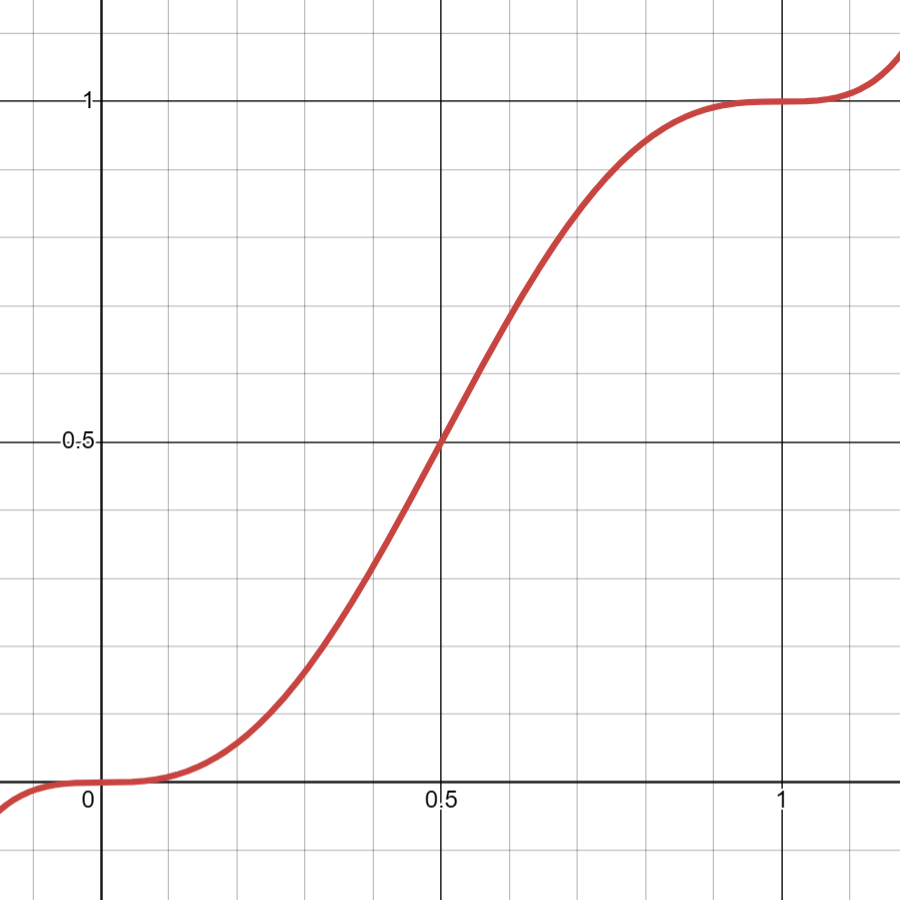
这一函数的最大特点在于其在 $x=0$ 与 $x=1$ 处二阶导都为0，这给予了其平滑边界过渡的功能。

这一 Fade 函数不仅仅可以被用于柏林噪声的实现，在其他例如值噪声、单形噪声的实现中，其也发挥着重要的作用。

Grad函数

private static float Grad(int hash, float x, float y)
{
    int h = hash & 7; // convert the hash to 0-7
    float u = h < 4 ? x : y;
    float v = h < 4 ? y : x;
    return (h & 1) == 0 ? u : -u + (h & 2) == 0 ? v : -v;
}

Grad函数实现了计算给定点的梯度值的功能；其第一眼看上去可能会令人有些困惑，在前面的原理叙述中，笔者描述的计算梯度值的方式是先给晶格点指定随机梯度向量，再使用点乘计算对应梯度值，但在这个函数中似乎既没有向量也没有点乘；实际上，这个函数确实实现了计算梯度值的功能，但在具体路径上进行了一些简化与优化。

如果我们对返回值情况进行枚举，这个函数的话其实可以将其转化为下面的这样：

private static float Grad(int hash, float x, float y)
{
    int h = hash & 7; // convert the hash to 0-7
    switch (h)
    {
        case 0: return x + y;
        case 1: return y - x;
        case 2: return x - y;
        case 3: return - x - y;
        case 4: return x + y;
        case 5: return y - x;
        case 6: return x - y;
        case 7: return - x - y;
        default: return 0;
    }
}

在Grad函数中，hash即为给定的晶格点，而我们可以进行预设，使得梯度向量的两个分量的绝对值都为1，即梯度向量只能为(1, 1)、(1, -1)、(-1, 1)、(-1, -1)之一，这样便可以将向量之间的点乘转化为加减法运算，可以显著提升性能表现并简化代码。而输入的x、y则为给定点到晶格点的距离向量，如此一来，最后的梯度值便可以简化为x + y、x - y、y - x、- x - y

Noise函数

public static float GetNoise(float x, float y)
{
    // the grid cell coordinates
    int gridX = Floor(x) & 255;
    int gridY = Floor(y) & 255;
    // the relative coordinates of the point in the cell
    float dx = x - Floor(x);
    float dy = y - Floor(y);
    // fade the relative coordinates
    float u = Fade(dx);
    float v = Fade(dy);
    // hash coordinates of the 4 corners
    int hashA = Permutation512[gridX] + gridY;
    int hashB = Permutation512[gridX + 1] + gridY;
    // bilinear interpolation
    float y0 = Lerp(Grad(Permutation512[hashA], dx, dy), Grad(Permutation512[hashB], dx - 1, dy), u);
    float y1 = Lerp(Grad(Permutation512[hashA + 1], dx, dy - 1), Grad(Permutation512[hashB + 1], dx - 1, dy - 1), u);
    return Lerp(y0, y1, v);
}

终于到了Noise函数了，这是算法的核心部分，从中可以一窥柏林算法的运算方式。

其中我们先通过Floor函数获取了给定坐标 $(x, y)$ 所处晶格的哈希索引，即gridX与gridY，通过它们我们便可以确定晶格中四个点的哈希值，即hashA、hashB、hashA+1与hashB+1，进而得到其对应梯度向量。

而之后，我们获得了dx与dy，它们是x与y在晶格中的相对位置，取值范围为 $[0,1)$ ，而之后的由Fade函数计算得到的u、v便是dx、dy的映射值。

最后便是通过Grad计算梯度值并使用双线性插值得到最后的噪声值。

下图可以清晰表示出这些变量的关系以及梯度值的计算方法：

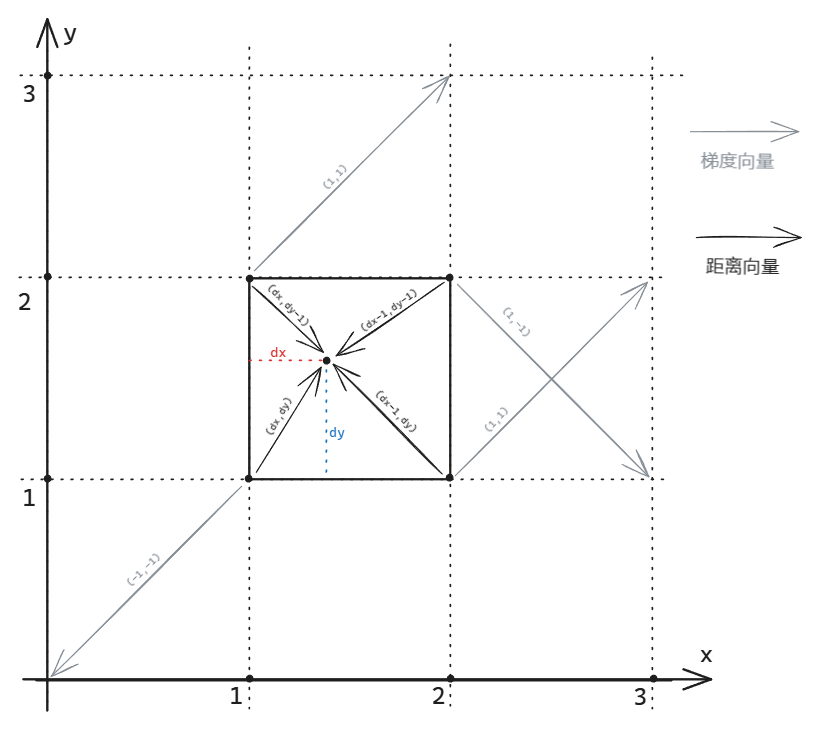
以上便是关于柏林噪声具体实现的论述，接下来笔者将尝试将柏林函数应用到实际的程序化生成中。

2D Tilemap生成

在理解了柏林噪声的原理，并实现了获取相应柏林噪声的算法之后；接下来，让我们将其应用到实际场景中试试吧！

笔者在Unity中实现了几个使用柏林噪声进行程序化地图生成的例子，其中包括2D Tilemap生成、3D地形生成等，以下项目与代码都可以在这个Github仓库中找到：

https://github.com/hmxsqaq/Unity-ProceduralMapGenerationPerlinNoise

获取噪声图

对于2D Tilemap的生成而言，柏林算法的应用非常直观，其噪声图本身便可以被描述为一张二维图像，如下所示

我们只需要将这张二维图像转化为数据，再将数据映射到Tilemap上即可。

首先我们需要获取到所需的噪声的数据，下图所示代码实现了这一功能：

public static float[,] GetNoiseMap(int seed, int width, int height, float scale)
{
    Random.InitState(seed);
    // init map
    float[,] noiseMap = new float[width, height];
    // avoid scale = 0;
    scale = scale <= 0 ? 0.0001f : scale;
    // get offset point
    Vector2 offset = new Vector2(Random.Range(-9999f, 9999f), Random.Range(-9999f, 9999));

    for (int y = 0; y < height; y++)
    {
        for (int x = 0; x < width; x++)
        {
            float sampleX = x / scale + offset.x;
            float sampleY = y / scale + offset.y;
            noiseMap[x, y] = PerlinNoise.GetNoise(sampleX, sampleY);
        }
    }
    return noiseMap;
}

在上面的代码中，我们先指定了seed，确定了使用的随机序列；使用offset作为偏移量、scale作为缩放来获取噪声，并将获取到的噪声值写入了二维数组noiseMap中；下图直观展示了offset与scale的定义：

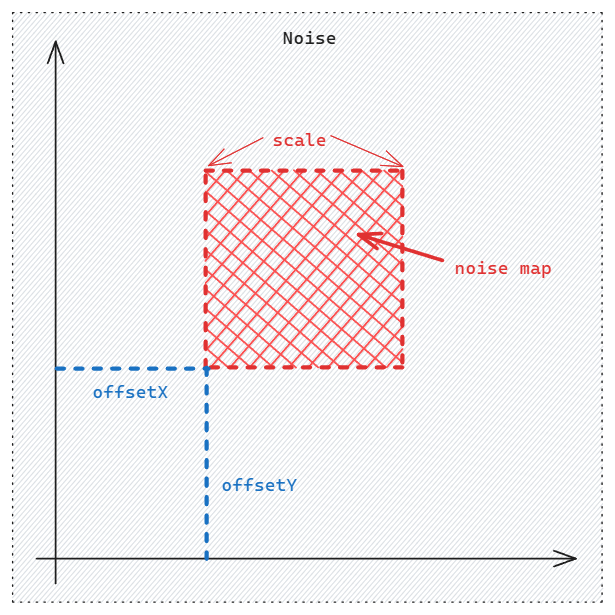
在获取噪声图的过程中，我们可以将柏林噪声函数理解为一张无限大的噪声图，而我们需要做的就是从这个坐标系中截取一个矩形（采样），而offset决定了我们截取（采样）的初始点，其由随机数进行指定；scale则决定了我们会截取原噪声图上多大的面积（实际上这并不准确，面积还由需要生成的噪声图的大小决定，scale最准确的描述应是“采样频率”），即我们会看到原噪声图的细致程度，scale越小，得到的噪声图越细致。

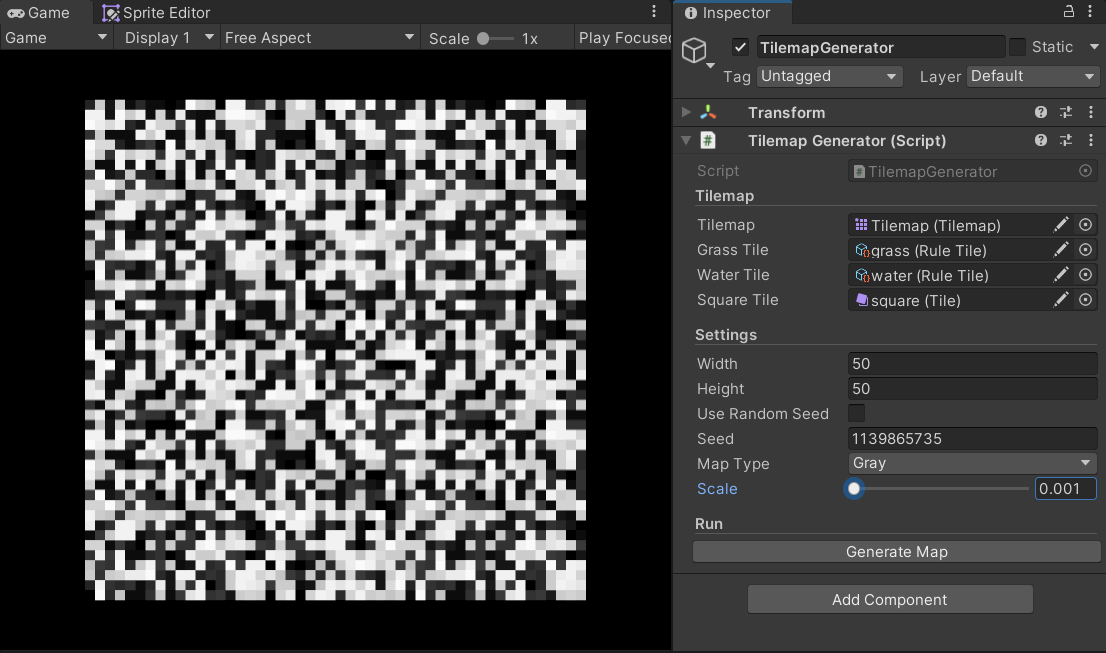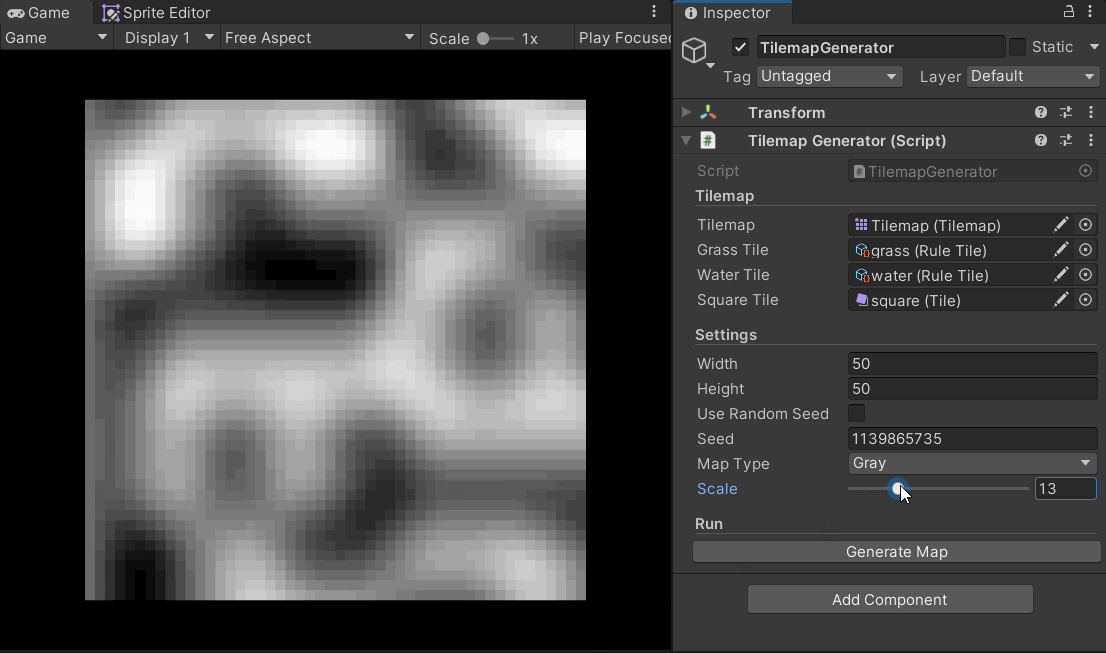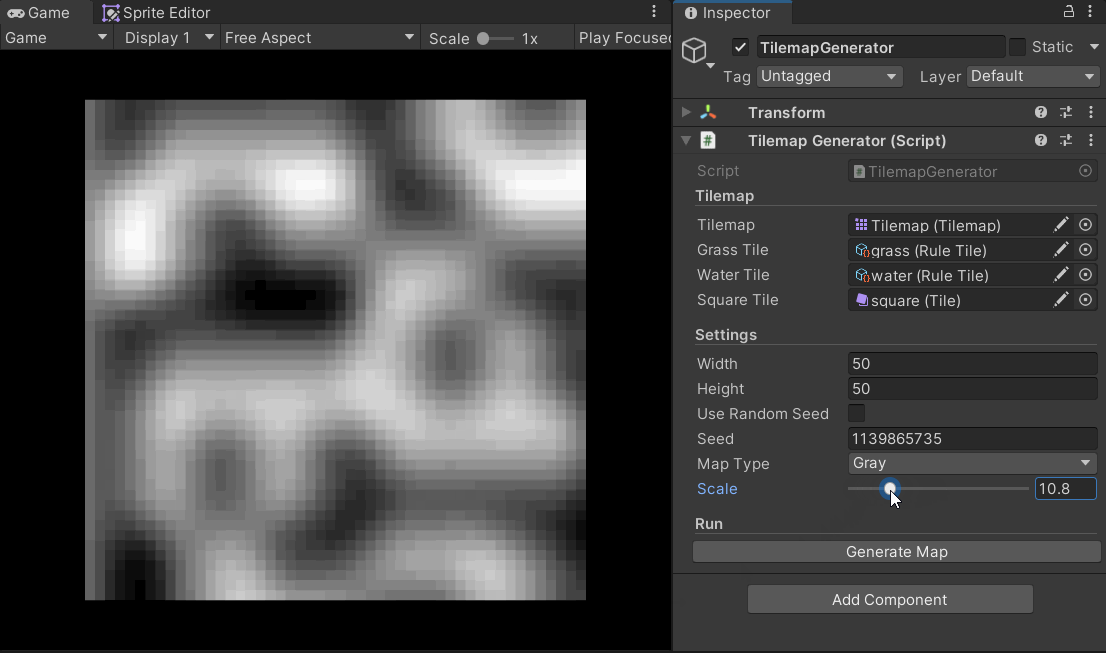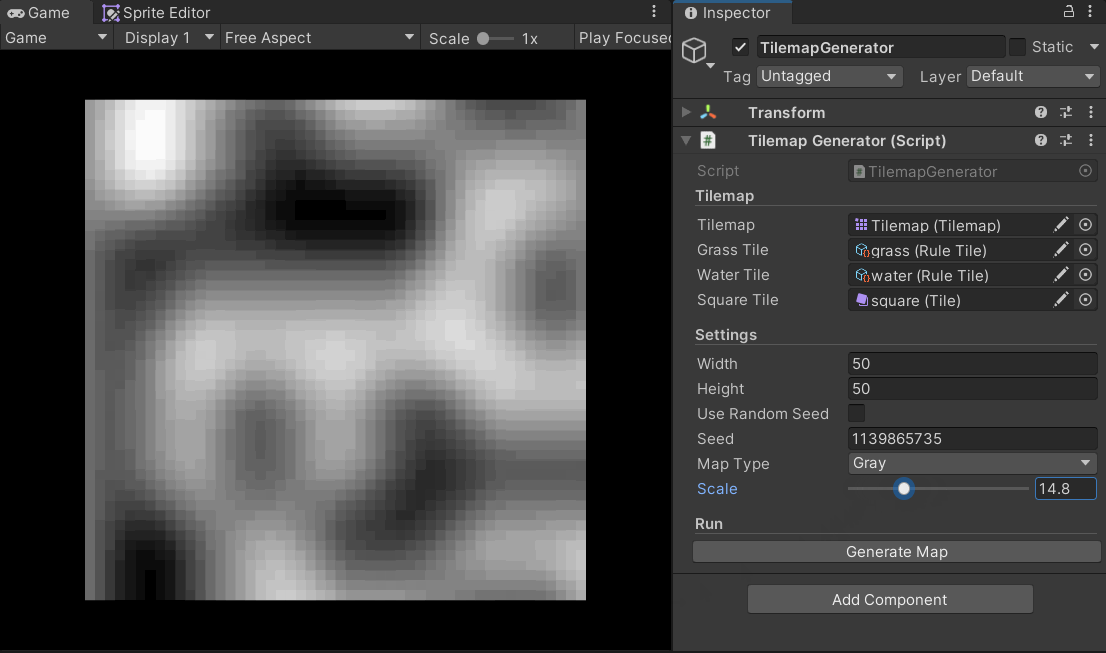
下面的gif图很好地呈现了scale对于噪声图的影响：

生成Tilemap

在获取了噪声图之后，我们要干的事情实际上就很简单了，根据将噪声图的数据映射到Tilemap上即可。我分别使用灰度图和网络中的素材实现了这一功能（上面的gif便是由灰度图的实现，这里不再重复展示）。

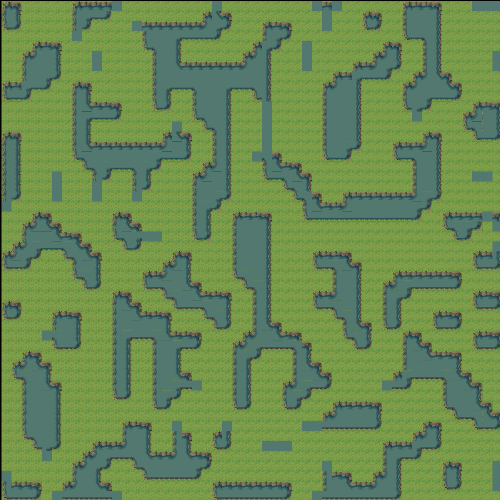
可以使用scale与waterProbability两个参数修改随机出的效果。

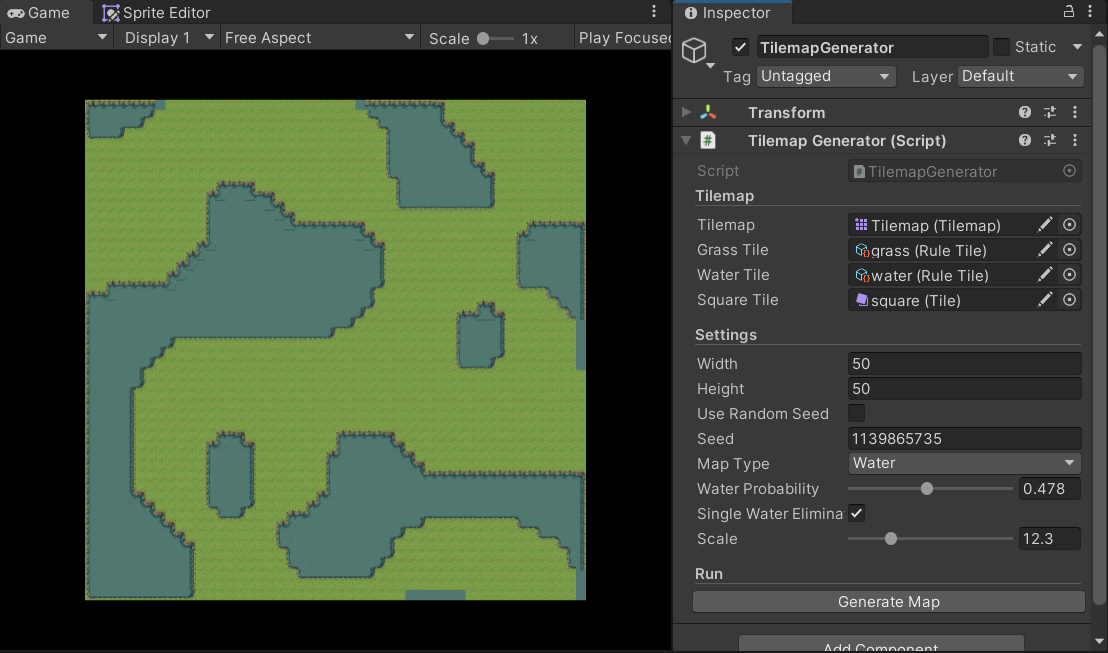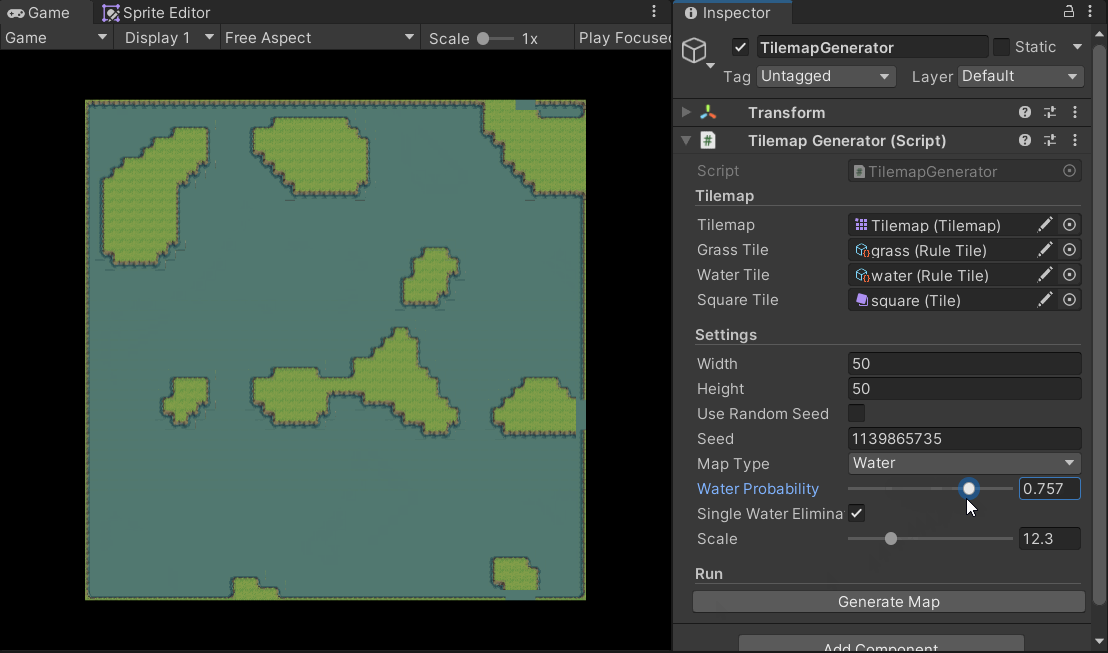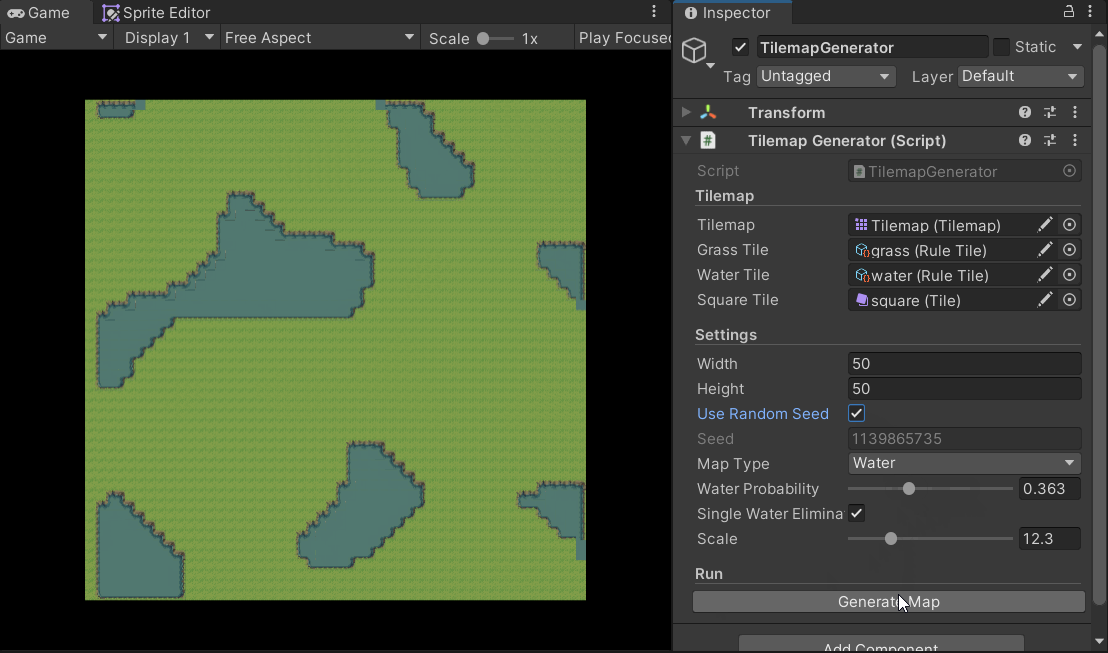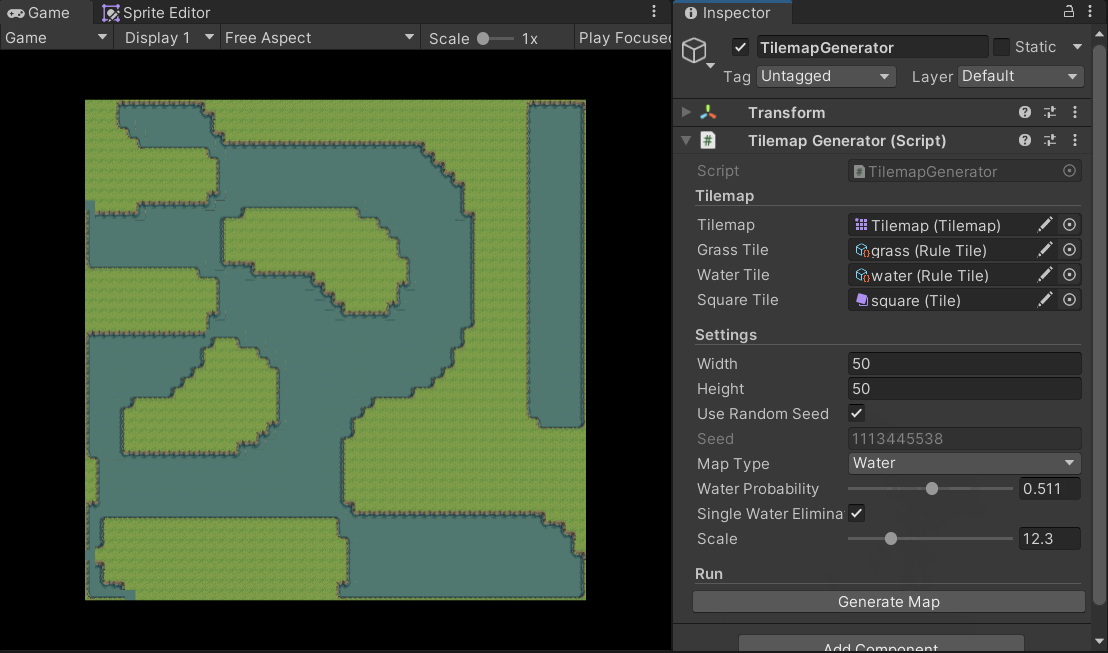
需要注意的是，我是用了Unity中的Rule Tile功能实现了瓦片的自适应。

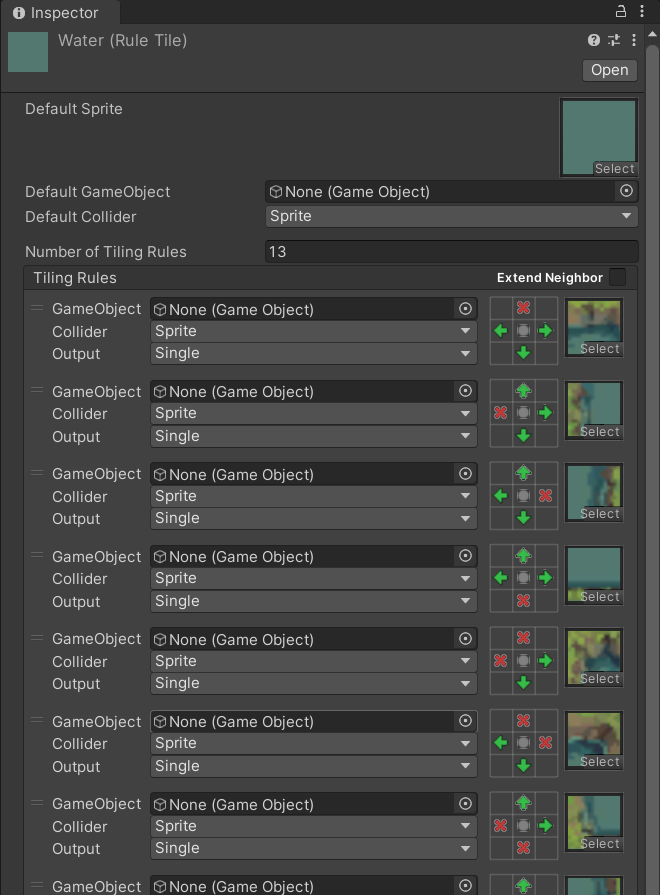
生成效果优化

如果我们仔细观察我们现在生成的地形，可以发现一些因为不太和谐的地方：

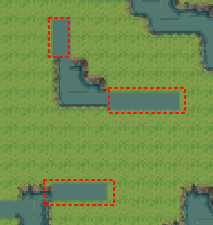
如上图全出的这些地方，它们的规则瓦片并没有被正常匹配，这是因为素材并没有提供对应的瓦片，但是我们可以对噪声图进行处理来剔除掉这些无法匹配的区块。

这些区块一个很重要的特点便是延伸过长，我们只需遍历每个点，检查其四周的区块分布情况即可，代码如下所示：

private void EliminateSingleWater()
{
    while (true)
    {
        bool hasSingleWater = false;
        for (int w = 0; w < width; w++)
        {
            for (int h = 0; h < height; h++)
            {
                if (!(NoiseMap[w, h] < waterProbability) || !CheckAroundHavePairLand(w, h)) continue;
                NoiseMap[w, h] = 1;
                hasSingleWater = true;
            }
        }

        if (!hasSingleWater) break;
    }
}

private bool CheckAroundHavePairLand(int x, int y)
{
    bool left = false, right = false, up = false, down = false;
    if (x > 0) left = NoiseMap[x - 1, y] > waterProbability;
    if (x < width - 1) right = NoiseMap[x + 1, y] > waterProbability;
    if (y > 0) up = NoiseMap[x, y - 1] > waterProbability;
    if (y < height - 1) down = NoiseMap[x, y + 1] > waterProbability;
    return (left && right) || (up && down);
}

这里使用了循环进行一层一层的剔除，其会带来一些额外的性能开销，但是确实可以提升生成的准确性。

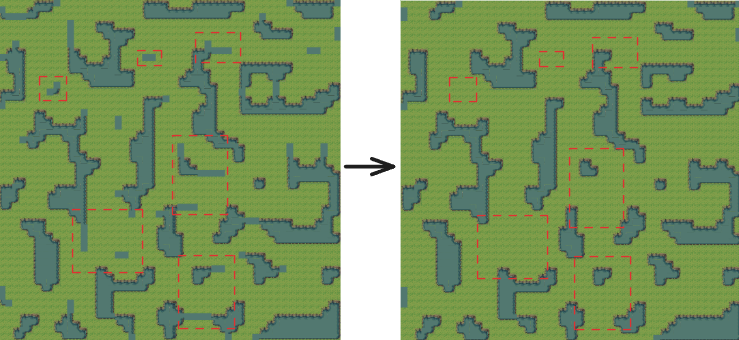
总结

在这里的实践中，我使用了一张噪声图与Tilemap中的Rule Tile实现了生成随机2D Tilemap地图的效果，并剔除了Rule Tile无法支持的瓦片，使得最后的地图效果更好。

3D类山地地形生成

以上是对于柏林噪声的非常基础的应用，其虽然简单，但是可以作为一个很好的开始；而在《Minecraft》这些游戏中，对与噪声的应用往往更加复杂更加综合，它们往往会用到多种噪声算法并生成多张噪声图以应对多种不同的需要，如《Minecraft》中就使用多张分形柏林噪声生成了湿度图、温度图、群系图等多种用处不一的噪声图。

接下来，笔者将更加深入地探索柏林噪声的应用，从Texture出发，实现更加符合现实的3D山地地形的程序化生成。

下面所用到的所有代码也都可以在这个Github仓库中找到：

https://github.com/hmxsqaq/Unity-ProceduralMapGenerationPerlinNoise

高度图Texture与着色Texture

在应对3D山地地形生成时，因为由原先的2D变为了3D，着色层面上，我们需要先依据噪声图获取到对应Texture来实现对山体的着色。

我们使用的逻辑和上面的2D Tilemap生成非常相似，只是将Tilemap替换为了Texture，得到的效果如下所示。

通过更细致地配置颜色梯度，我们便可以得到更加好的地形图效果。

分形柏林噪声

我们使用多层的颜色地图与柏林噪声尝试创造了地形图，其呈现了一定的随机梯度，但是其实际效果并不逼真，其显得有些太过于“平滑”了，缺少了许多的细节，而我们的自然界实际上并不那么平滑。分形柏林噪声可以一定程度上解决这一问题。

分形是指具有自相似性的复杂结构，即在不同尺度上看起来相似的图案。在自然界中，许多现象（如山脉、海岸线、云层等）都具有分形特征。分形柏林噪声结合了柏林噪声和分形的概念。具体来说，它通过多次叠加不同频率和振幅的柏林噪声来生成更加复杂和自然的噪声模式。这种叠加通常称为“Octaves”（倍频）。每个倍频层次的柏林噪声具有不同的频率和振幅，频率通常是前一个层次的两倍，振幅则是前一个层次的一半。通过叠加多个倍频层次，分形柏林噪声能够生成具有多尺度细节的复杂图案。

我们将在噪声图生成算法中引入一些额外参数来实现分形柏林噪声：

octaves：倍频程数，决定噪声的细节层次
persistence：每个倍频程的振幅缩减因子
lacunarity：每个倍频程的频率增加因子

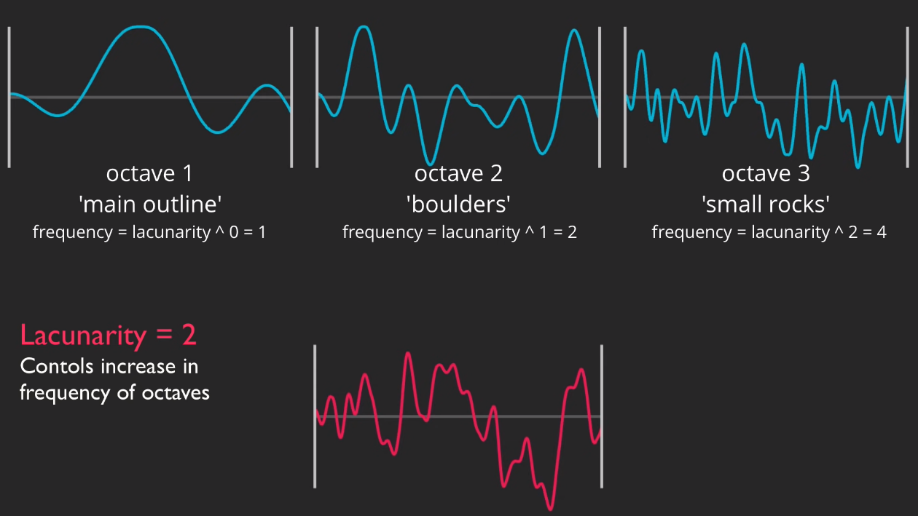
我的实现如下所示：

public static float[,] GetNoiseMap(int seed, int width, int height, float scale, Vector2 offset,
                                   int octaves = 1, float persistance = 1, float lacunarity = 1)
{
    Random.InitState(seed);
    // init map
    float[,] noiseMap = new float[width, height];
    // avoid scale <= 0
    scale = scale <= 0 ? 0.0001f : scale;
    // get offset point
    Vector2[] octavesOffsets = new Vector2[octaves];
    for (int i = 0; i < octaves; i++)
        octavesOffsets[i] = new Vector2(Random.Range(-9999f, 9999f), Random.Range(-9999f, 9999)) + offset;
    // store min and max value for normalization
    float minNoise = float.MaxValue;
    float maxNoise = float.MinValue;
    // store half width and height for centering the noise map
    float halfWidth = width / 2f;
    float halfHeight = height / 2f;

    for (int y = 0; y < height; y++)
    {
        for (int x = 0; x < width; x++)
        {
            float amplitude = 1;
            float frequency = 1;
            float noise = 0;

            for (int i = 0; i < octaves; i++)
            {
                float sampleX = (x - halfWidth) / scale * frequency + octavesOffsets[i].x;
                float sampleY = (y - halfHeight) / scale * frequency + octavesOffsets[i].y;
                float perlinNoise = PerlinNoise.GetNoise(sampleX, sampleY) * 2 - 1;
                noise += perlinNoise * amplitude;

                amplitude *= persistance;
                frequency *= lacunarity;
            }
            // get min and max noise value to lerp
            if (noise < minNoise) minNoise = noise;
            if (noise > maxNoise) maxNoise = noise;
            noiseMap[x, y] = noise;
        }
    }

    // normalize the noise map
    for (int y = 0; y < height; y++)
        for (int x = 0; x < width; x++)
            noiseMap[x, y] = Mathf.InverseLerp(minNoise, maxNoise, noiseMap[x, y]);

    return noiseMap;
}

其使用了累乘的方式对噪声图进行迭代，提供了多个可对噪声图进行调整的参数，如octaves、persistence、lacunarity、offset等；通过调整参数，可以生成各种不同特性的噪声纹理。

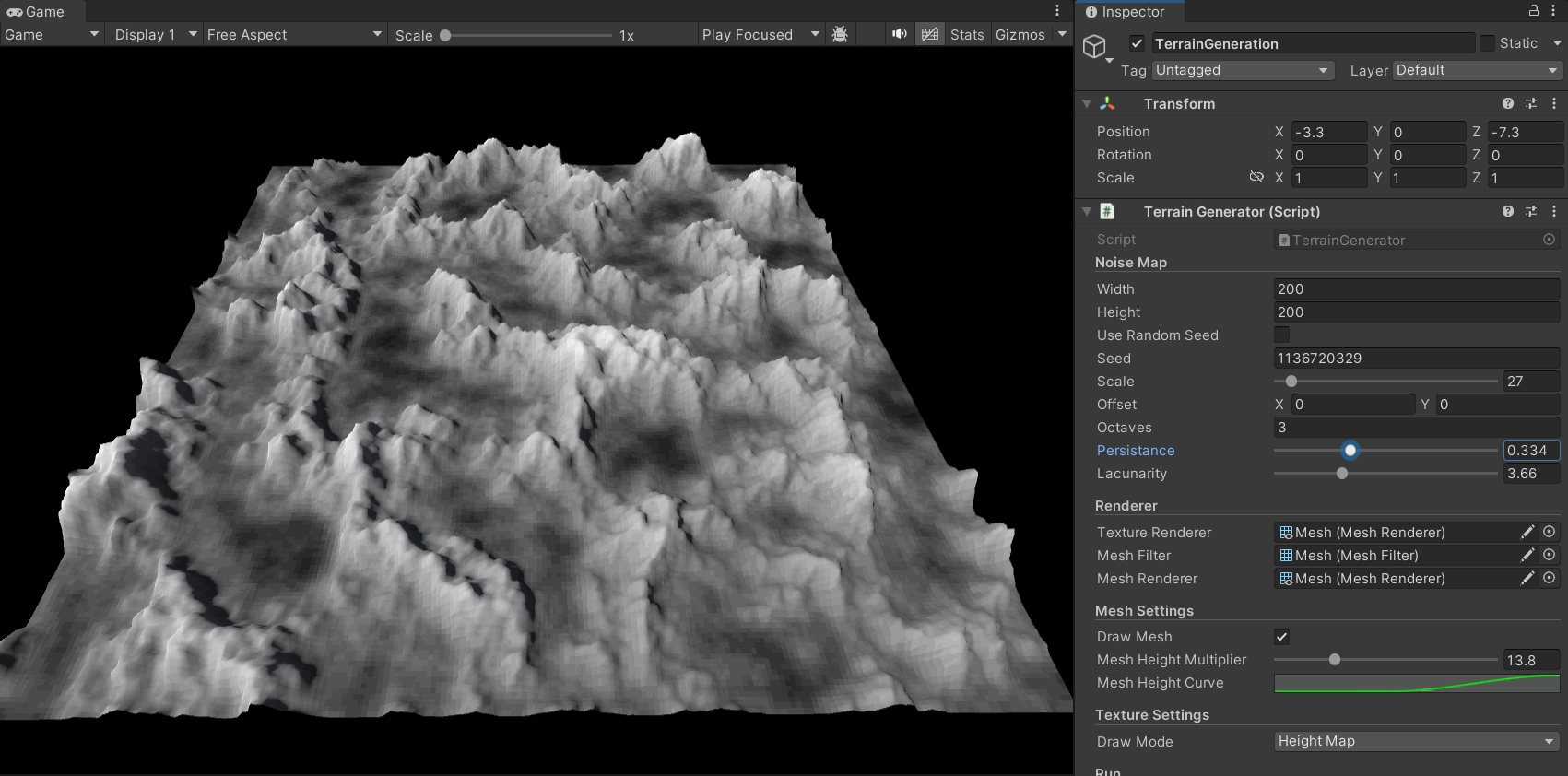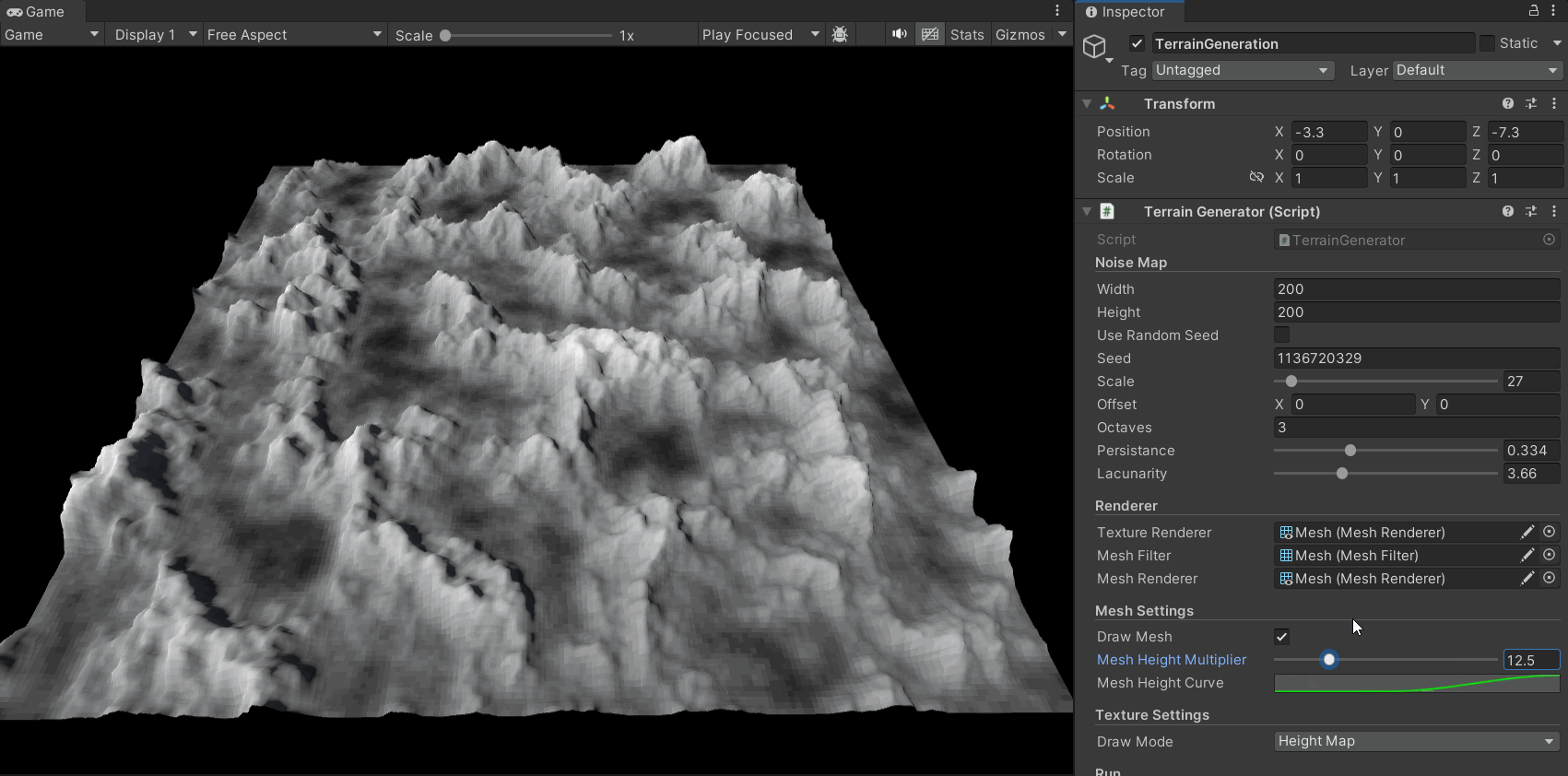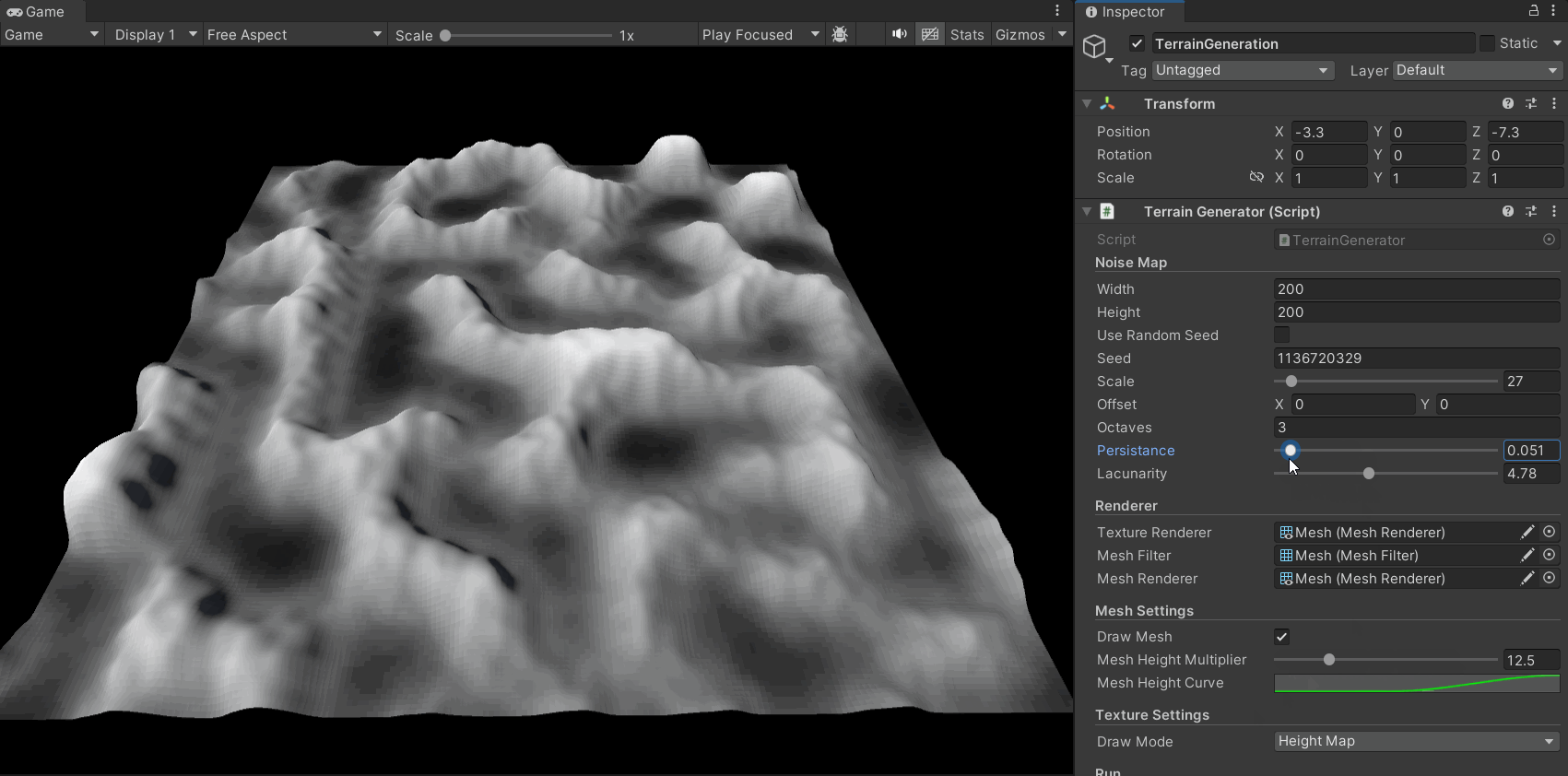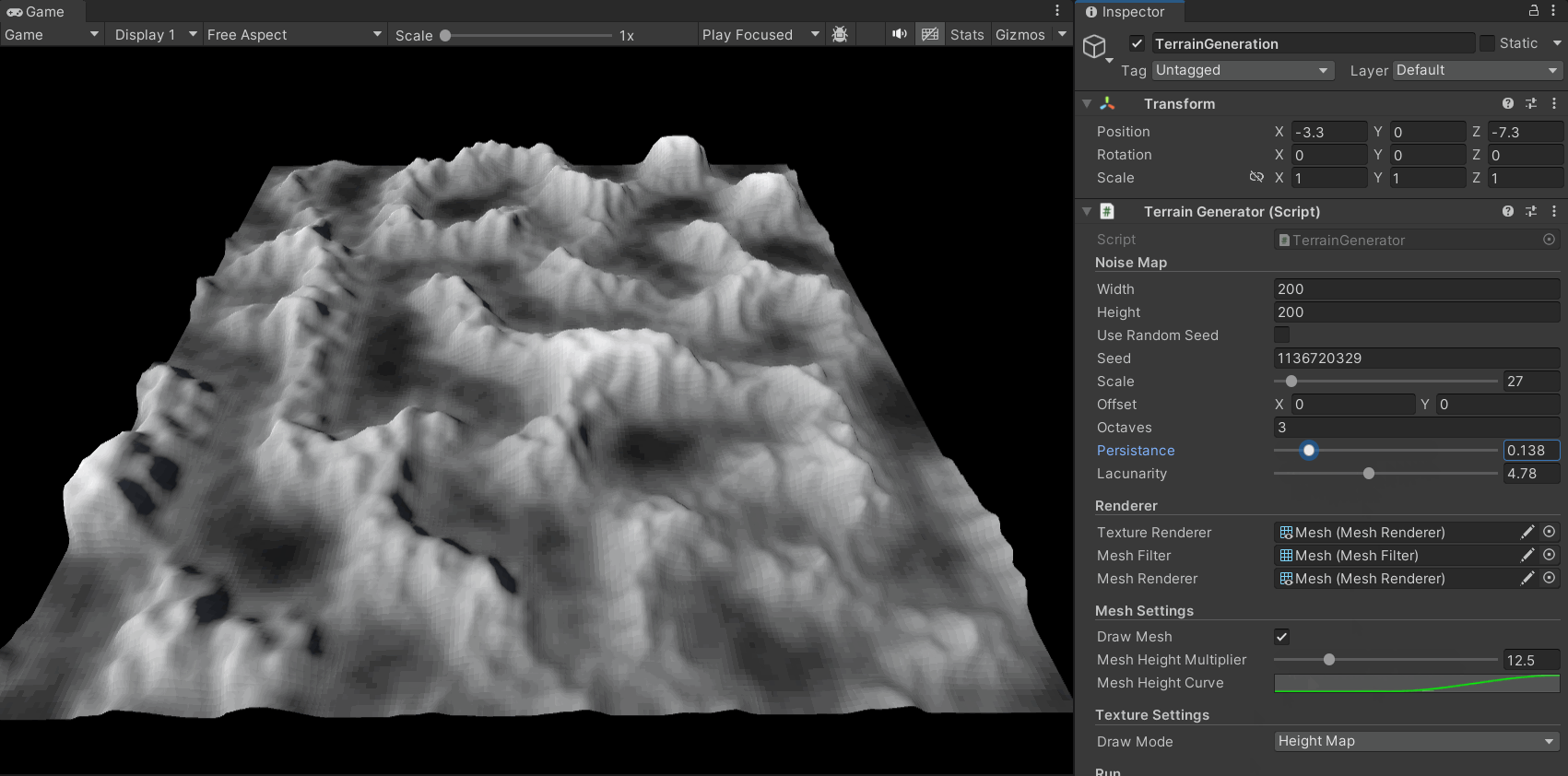
下面的gif展示了其效果：

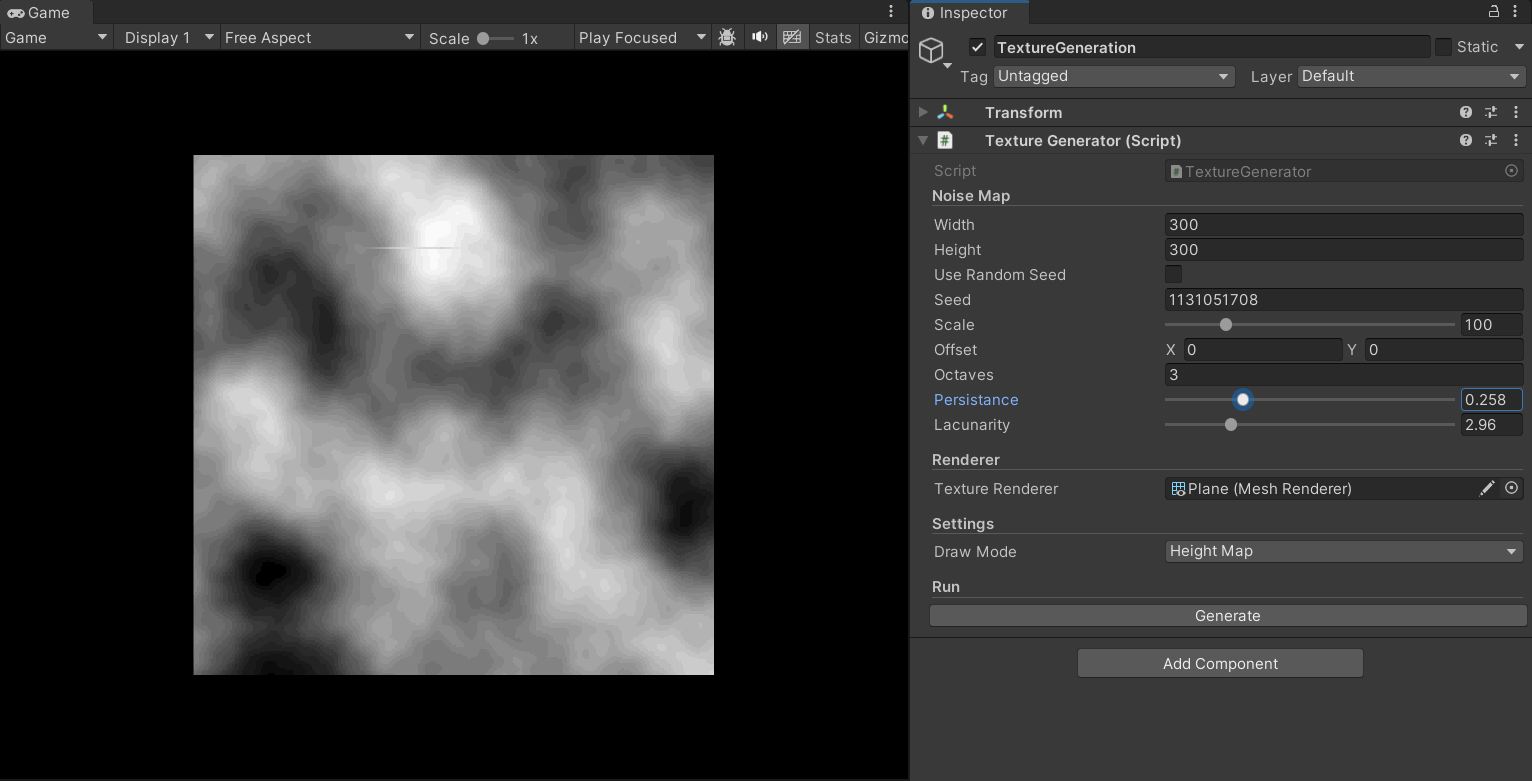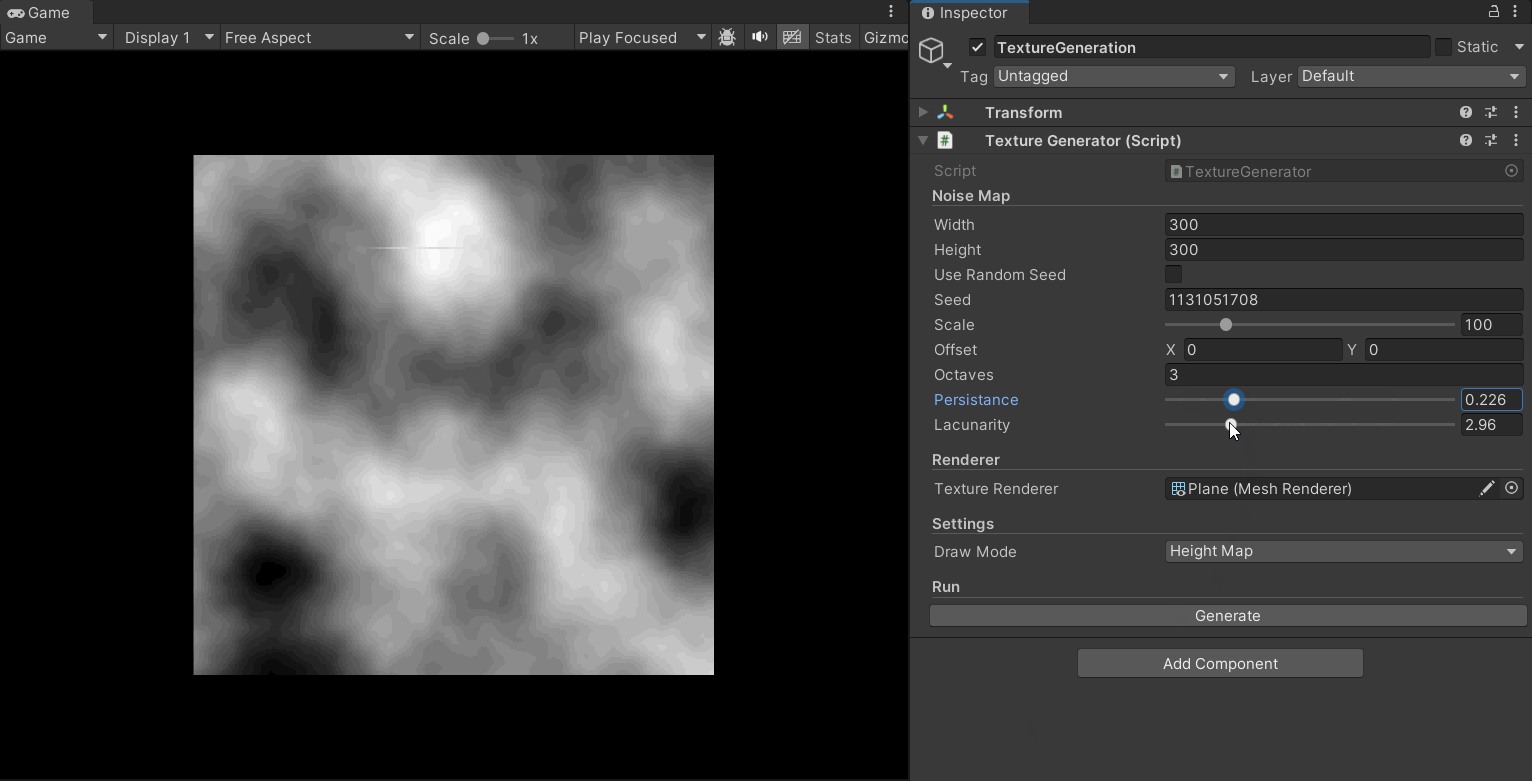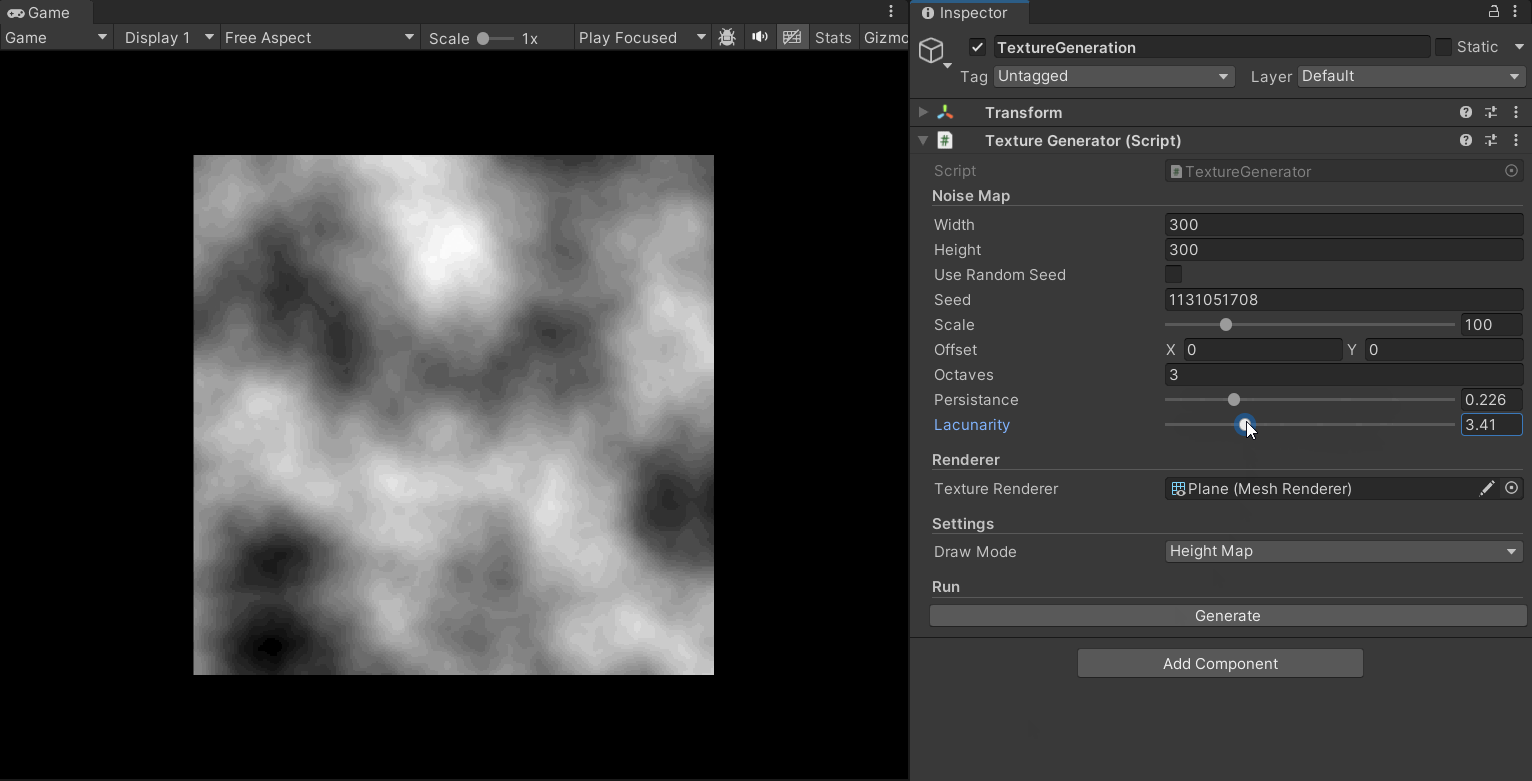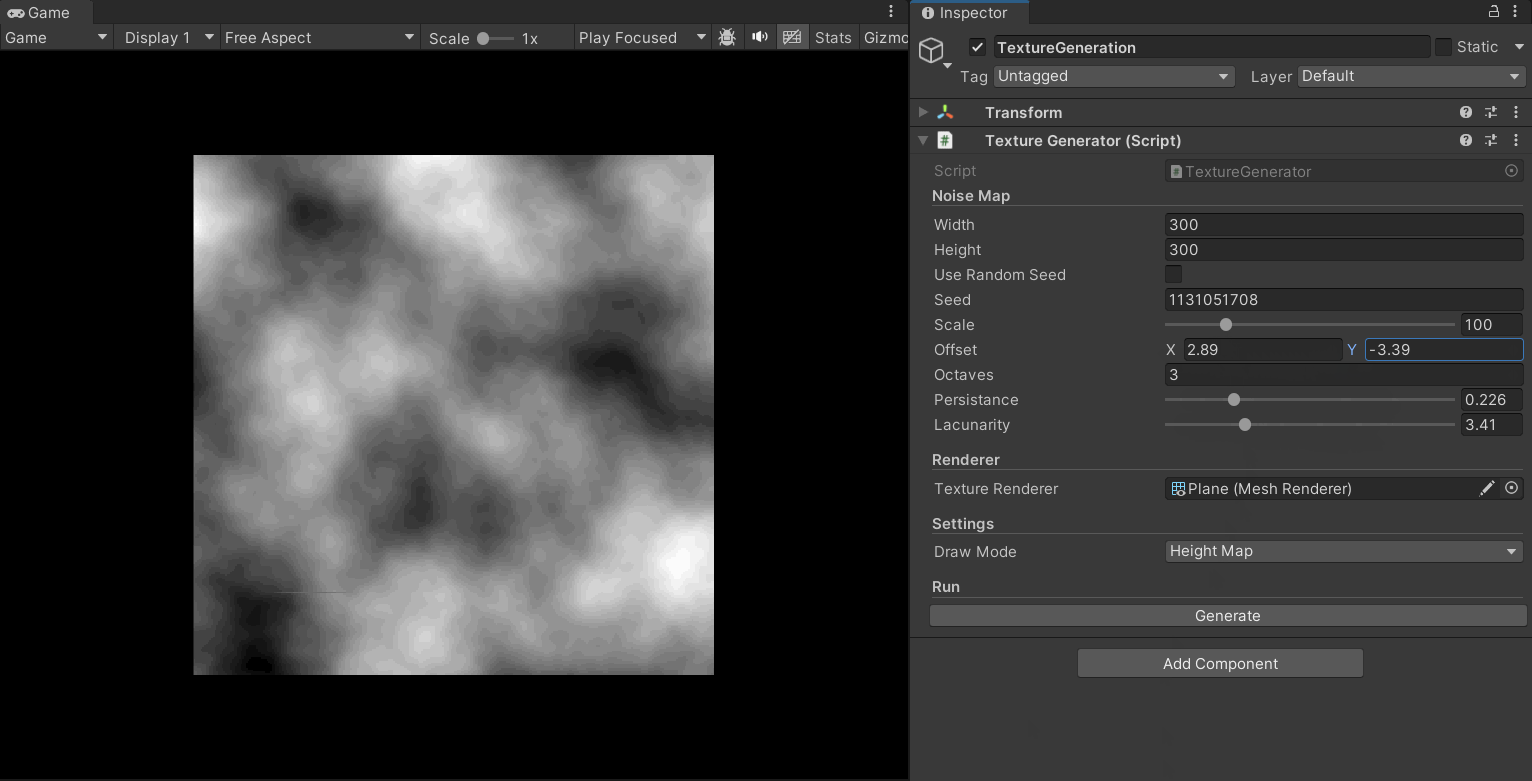
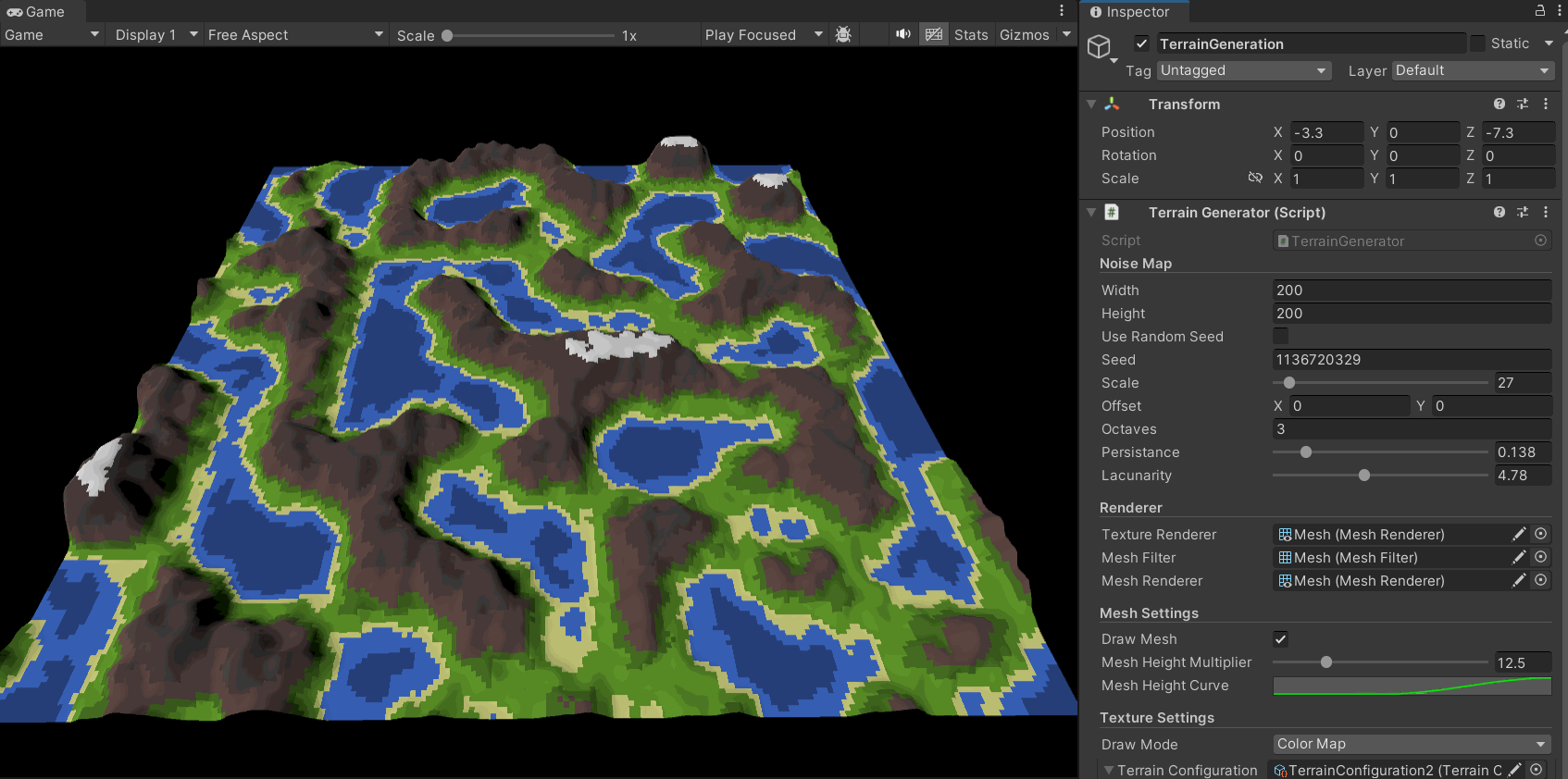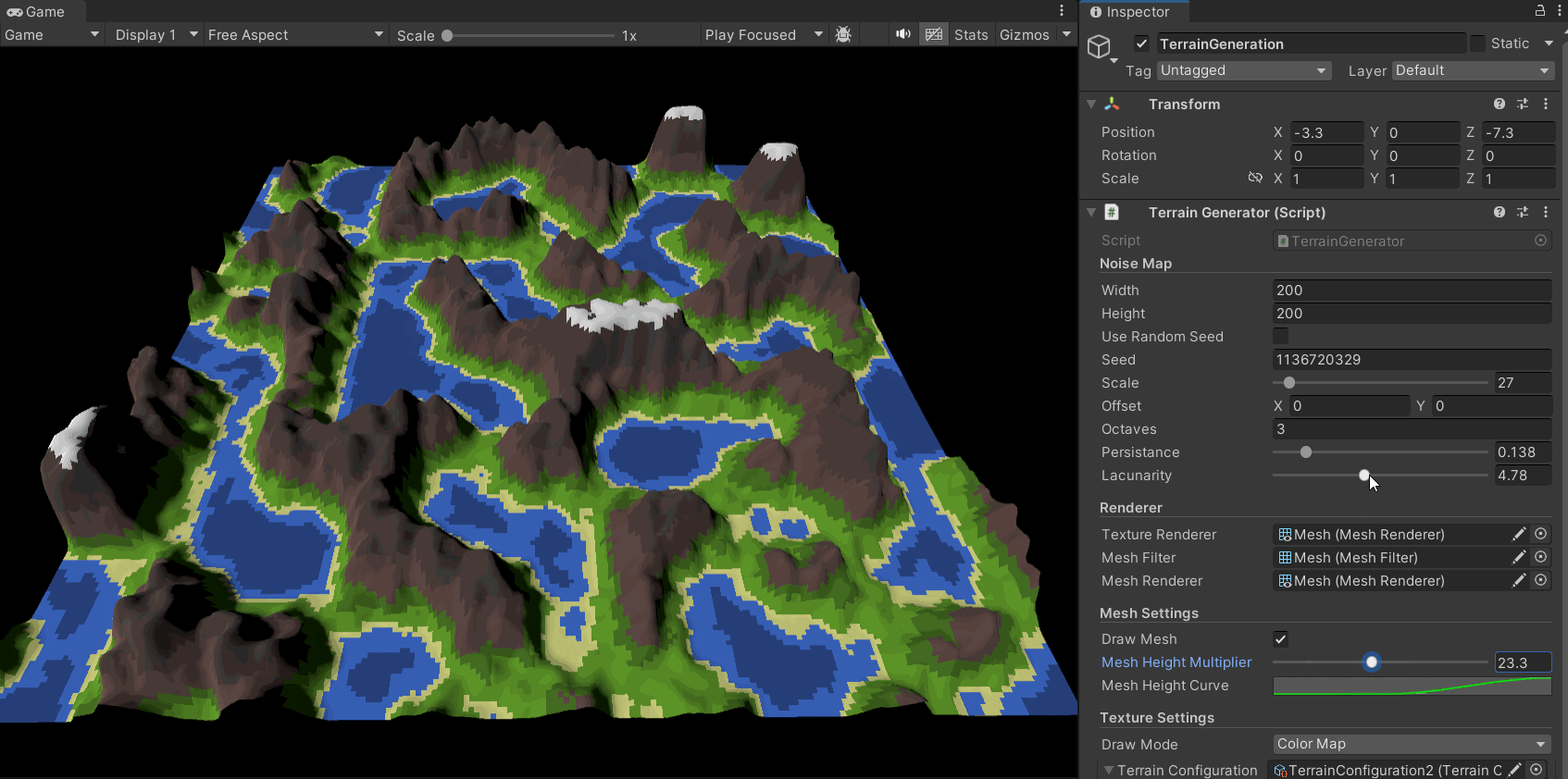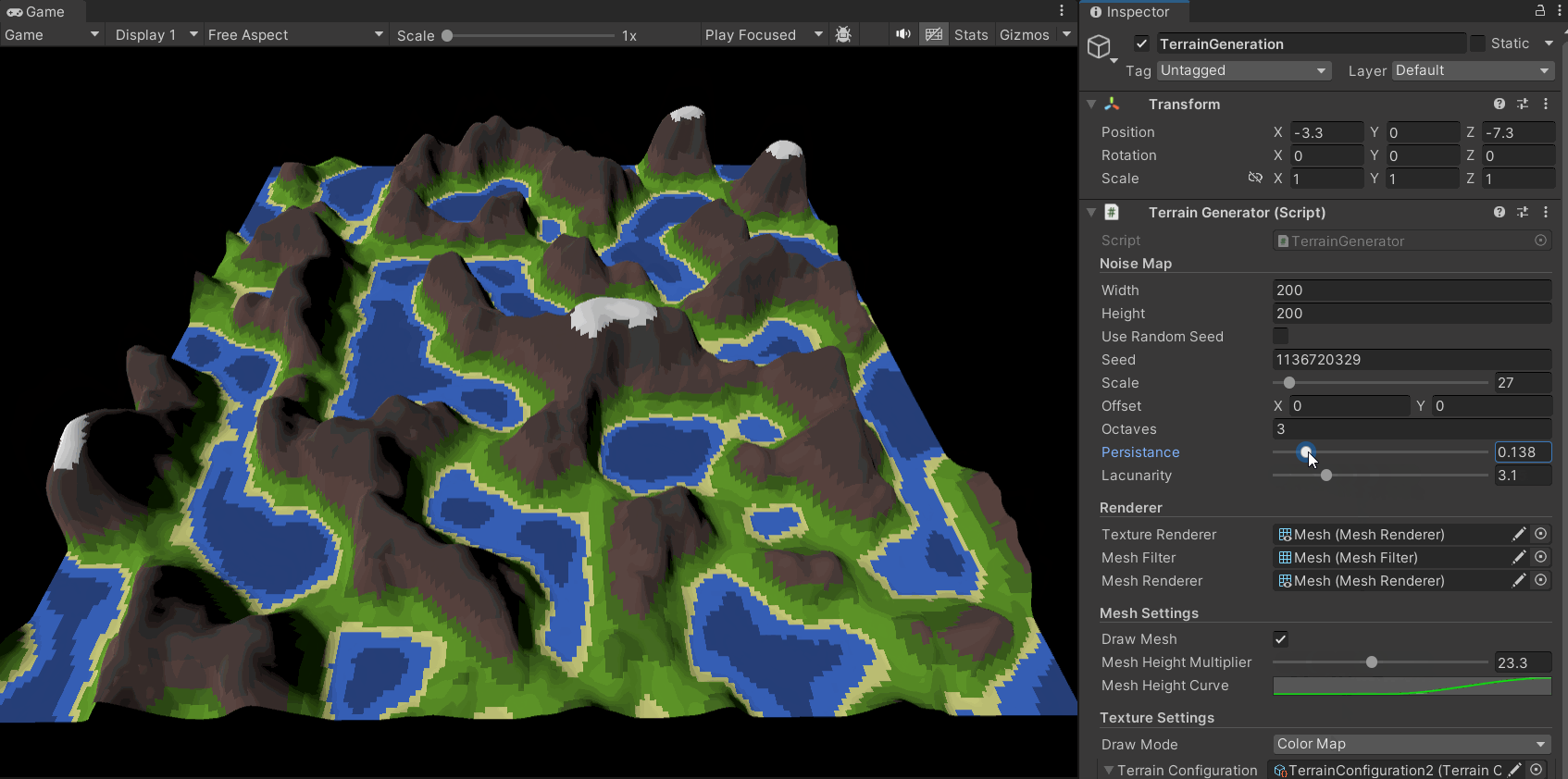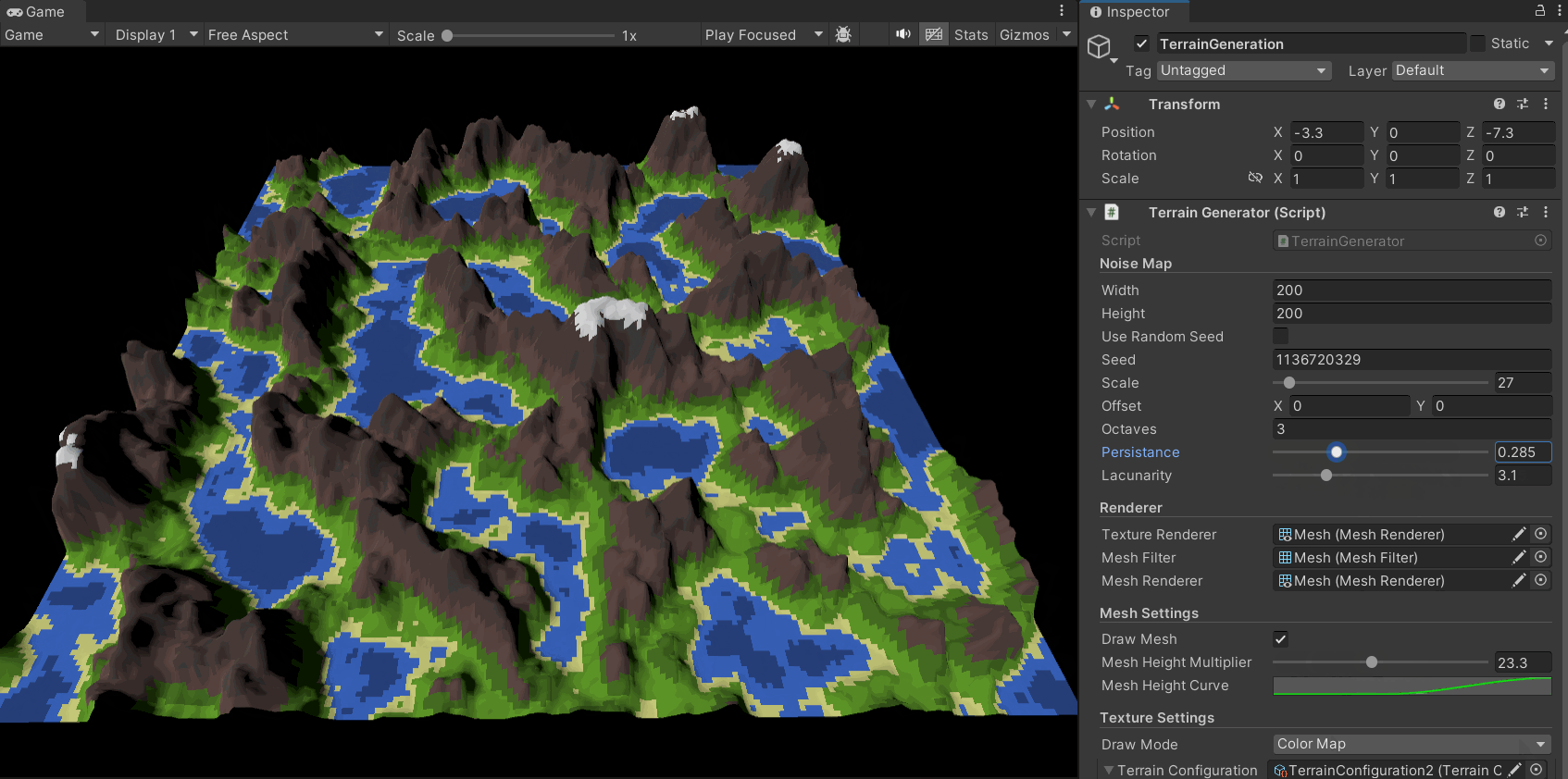
现在，在分形柏林算法加入后，地形图的生成效果有了很大的提升，其细节更加丰富，层次也更加多样：

同时，我们可以通过对参数的调整得到多种地形风格：

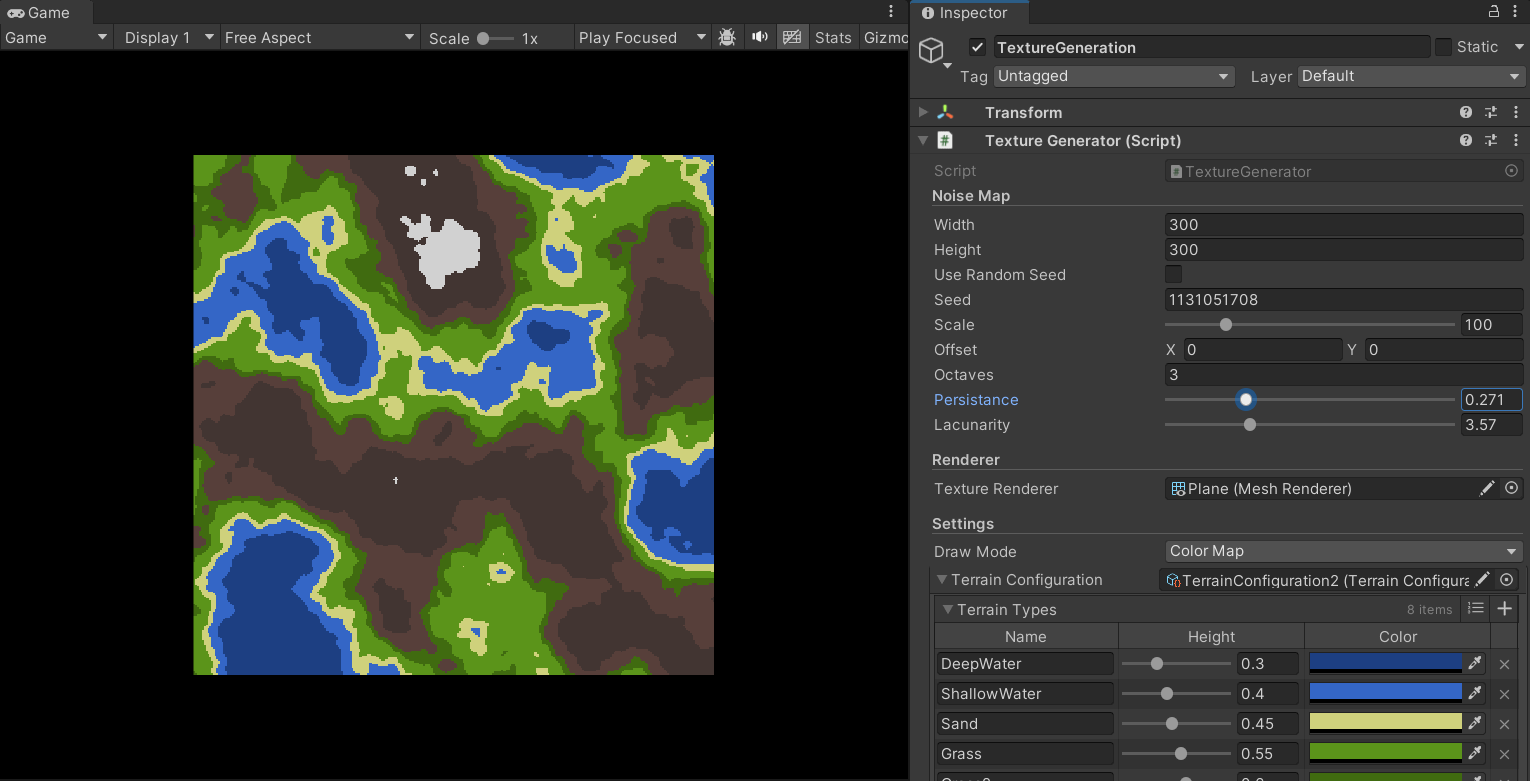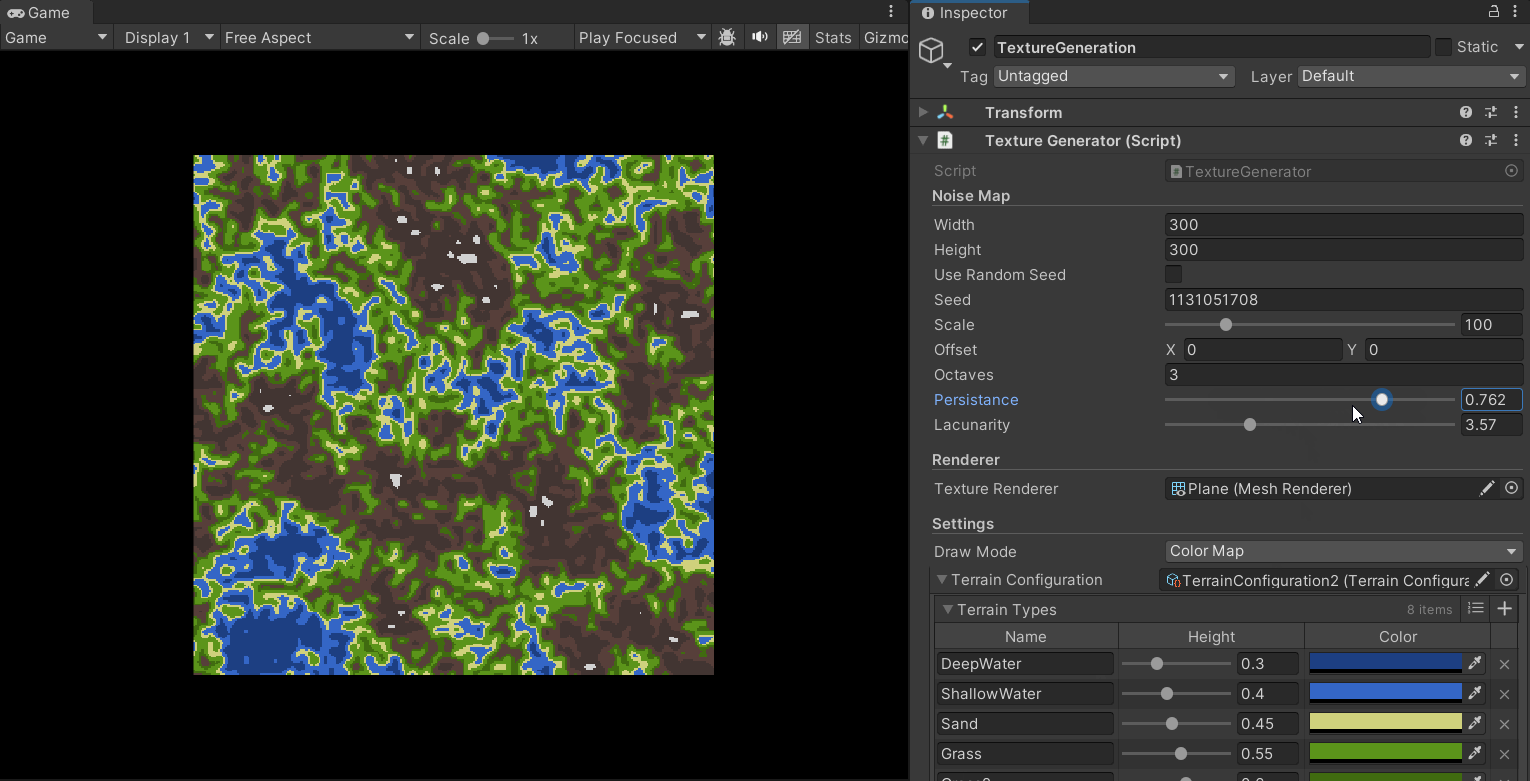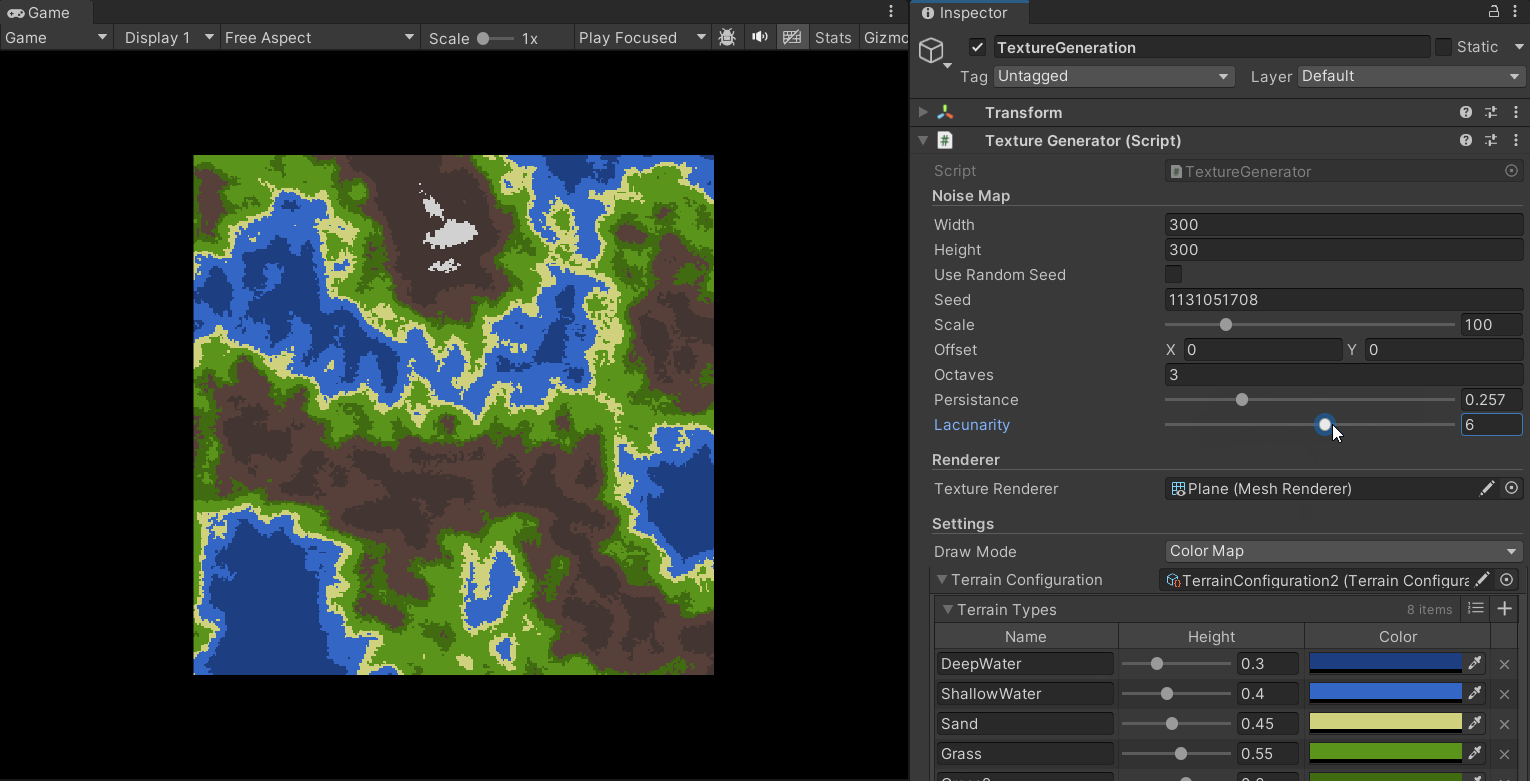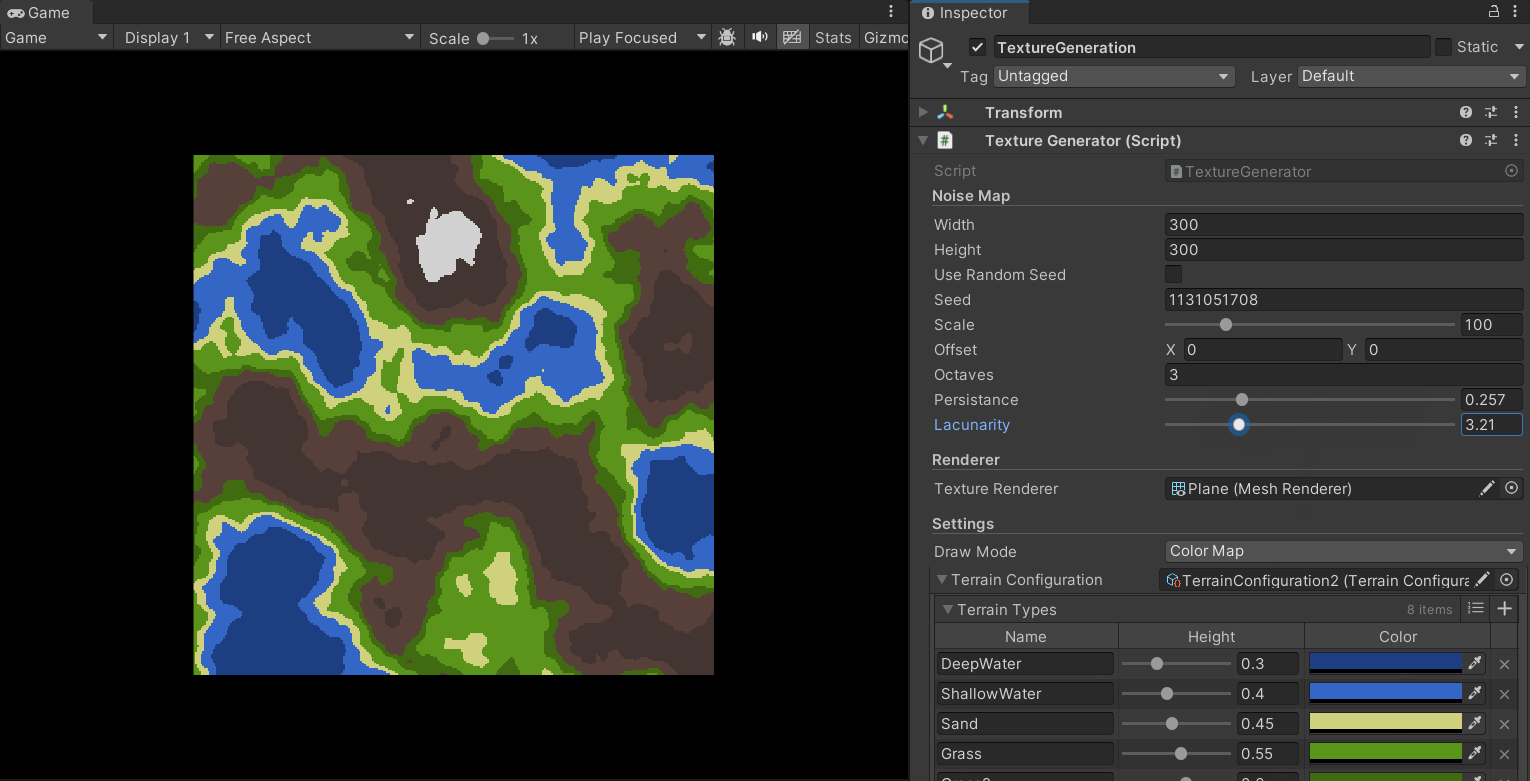
为地形赋予高度

在之前的实践中，笔者通过为plane设置Texture实现了基于噪声图的着色，而接下来，让我们为其赋予高度，使其成为真正的山地。

如下图所示，要实现这点的思路非常简单，我们之前已经得到了高度图，依据高度图设置plane的mesh即可实现地形的高度差。

如下面的代码所示，笔者依据噪声图进行了mesh数据的获取：

private static Mesh GenerateTerrainMesh(float[,] noiseMap, float heightMultiplier, AnimationCurve heightCurve)
{
    int width = noiseMap.GetLength(0);
    int height = noiseMap.GetLength(1);
    // get offset to center the mesh
    float topLeftX = (width - 1) / -2f;
    float topLeftZ = (height - 1) / 2f;

    MeshData meshData = new MeshData(width, height);
    int vertexIndex = 0;
    for (int y = 0; y < height; y++)
    {
        for (int x = 0; x < width; x++)
        {
            meshData.Vertices[vertexIndex] = new Vector3(topLeftX + x, heightCurve.Evaluate(noiseMap[x, y]) * heightMultiplier, topLeftZ - y);
            meshData.UVs[vertexIndex] = new Vector2(x / (float)width, y / (float)height);
            if (x < width - 1 && y < height - 1)
            {
                meshData.AddTriangle(vertexIndex, vertexIndex + width + 1, vertexIndex + width);
                meshData.AddTriangle(vertexIndex + width + 1, vertexIndex, vertexIndex + 1);
            }
            vertexIndex++;
        }
    }
    return meshData.CreateMesh();
}

同时，加入了heightMultiplier与heightCurve两个参数，其分别控制高度的系数与高度的变化曲线，使得我们可以更加细致地控制生成地形的效果。

如我们可以在heightCurve中将0~0.4都映射为0，这样可以保证海平面不会凸起或凹陷。

得到的效果如下所示：

其他程序化生成算法

在程序化地形生成中，除了基础柏林噪声外，还有许多其他算法也被广泛应用。本文将简要介绍其中的三种：Simplex 噪声、DLA算法与侵蚀算法。

Simplex 噪声

Simplex 噪声也是由 Ken Perlin 于2001年发明的一种改进的噪声函数，它旨在克服传统柏林噪声的一些缺点。

Simplex 噪声具有以下几个显著特点：

计算效率更高：柏林噪声在计算时需要为晶格赋予随机梯度，而随着维度的上升，需要计算的随机梯度数量会呈几何级上升，这让其在高维度下的性能难以让人接受；而Simplex 噪声在高维空间中的计算复杂度则要比柏林噪声低很多，这使得它在实时应用中更具优势。
视觉效果更好：Simplex 噪声在生成的图像中没有明显的轴对齐伪影（artifact），这使得生成的地形更加自然和逼真
更好的梯度分布：Simplex 噪声的梯度分布更加均匀，这有助于生成平滑过渡的地形。

Simplex 噪声的具体实现相对复杂，这里不做深入的研究，可以参考[这一论文](https://muugumuugu.github.io/bOOkshelF/generative art/simplexnoise.pdf)中给出的实现；但其核心思想并不复杂，是通过将输入空间划分为一系列的单形（如三角形或四面体），并在这些形状的顶点上生成随机梯度。然后，通过对这些梯度进行插值，生成最终的噪声值。