algorithm4

官网：https://algs4.cs.princeton.edu/home/

笔记目录：https://hmxs.games/posts/11300/

查找

查找便是尽可能高效地在数据集合中定位特定元素的过程，而现代计算机和网络使我们能够得以访问到极其海量的信息，这时，查找便显得极为重要。本章将介绍一些经典查找算法。

符号表（字典）是对于查找的抽象数据结构实现，其最主要的目的就是将一个键（key）和一个值（value）联系起来，通过键我们便可以快速访问到值，而其实现有着多种方式，如二叉查找树、红黑树、散列表等，在本章中将着重介绍它们。

使用了C++对查找算法进行了重新实现，在这一Github仓库下可以找到我的全部实现

顺序查找符号表 - Sequential search in an unordered linked list

这是最简单的一种对于符号表的实现：我们可以使用链表来存储数据，在我们需要获取数据时，我们只需要从头一个个查找过去即可。

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
template <typename KEY, typename VALUE>
class SequentialSearchSymbolTable {
public:
    ~SequentialSearchSymbolTable() {
        while (head_ != nullptr) {
            Node* old = head_;
            head_ = head_->next;
            delete old;
        }
    }

    void put(KEY key, VALUE value) {
        for (Node* x = head_; x != nullptr; x = x->next) {
            if (x->key == key) {
                x->value = value;
                return;
            }
        }
        head_ = new Node(key, value, head_);
        size_++;
    }

    std::optional<VALUE> get(KEY key) {
        for (Node* x = head_; x != nullptr; x = x->next) {
            if (x->key == key) {
                return x->value;
            }
        }
        return std::nullopt;
    }

    void remove(KEY key) {
        Node* previous = nullptr;
        for (Node* x = head_; x != nullptr; previous = x, x = x->next) {
            if (x->key == key) {
                if (previous != nullptr) {
                    previous->next = x->next;
                } else {
                    head_ = x->next;
                }
                delete x;
                size_--;
                return;
            }
        }
    }

    bool contains(KEY key) { return get(key).has_value(); }
    bool is_empty() { return head_ == nullptr; }
    size_t size() { return size_;}

private:
    struct Node {
        KEY key;
        VALUE value;
        Node* next;
        Node(KEY key, VALUE value, Node* next) : key(key), value(value), next(next) {}
    };

    Node* head_ = nullptr;
    size_t size_ = 0;
};

以上使用了C++简单地实现了一个顺序符号表，其使用了一个私有内部Node类来表示链表节点用于存储KEY与VALUE，get与put方法都会顺序地搜索链表查找给定值。

这种实现当然可以运行，但是其效率相对较低，其get与put方法都有着O(N)O(N)级别的时间复杂度，在面对大规模问题时会显得力不从心。

二分查找符号表 - Binary search in an ordered array

这种符号表的实现也较为简单，其通过一对平行数组，分别存储键与值，然后通过二分查找实现数据的插入与获取

通过使用二分查找替换遍历，这种实现可以将get方法的复杂度优化到logNlogN

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
template<Comparable KEY, typename VALUE>
class BinarySearchSymbolTable {
public:
    void put(KEY key, VALUE value) {
        int i = rank(key);
        if (i < keys_.size() && keys_[i] == key) {
            values_[i] = value;
            return;
        }
        keys_.insert(keys_.begin() + i, key);
        values_.insert(values_.begin() + i, value);
    }

    std::optional<VALUE> get(KEY key) {
        if (is_empty()) return std::nullopt;
        int i = rank(key);
        if (i < keys_.size() && keys_[i] == key) {
            return values_[i];
        }
        return std::nullopt;
    }

    void remove(KEY key) {
        if (is_empty()) return;
        int i = rank(key);
        if (i < keys_.size() && keys_[i] == key) {
            keys_.erase(keys_.begin() + i);
            values_.erase(values_.begin() + i);
        }
    }

    // returns the number of keys in this symbol table strictly less than key.
    int rank(KEY key) {
        int left = 0, right = keys_.size() - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2; // prevent integer overflow
            if (key < keys_[mid]) {
                right = mid - 1;
            } else if (key > keys_[mid]) {
                left = mid + 1;
            } else {
                return mid;
            }
        }
        return left;
    }

    std::optional<KEY> min() {
        if (is_empty()) return std::nullopt;
        return keys_.front();
    }

    std::optional<KEY> max() {
        if (is_empty()) return std::nullopt;
        return keys_.back();
    }

    std::optional<KEY> select(int k) {
        if (k < 0 || k >= keys_.size()) return std::nullopt;
        return keys_[k];
    }

    std::optional<KEY> ceiling(KEY key) { return select(rank(key)); }

    std::optional<KEY> floor(KEY key) { return select(rank(key) - 1); }

    bool contains(KEY key) { return get(key).has_value(); }

    bool is_empty() { return keys_.empty(); }

    size_t size() { return keys_.size(); }

private:
    std::vector<KEY> keys_;
    std::vector<VALUE> values_;
};

二叉查找树 - Binary Search Tree

在上面的实现中，二叉查找树很好地优化了算法的速度，但因为要使用二分查找这种实现使用了数组存储数据，但这会让put方法的效率不够令人满意

或许我们需要链式地存储数据才能让插入操作变得快捷，那么应该如何在链式存储中使用二分查找解决问题呢？这就轮到二叉查找树 - BST出场了

二叉查找树基于二叉树实现，其基本原理为每个结点的键都大于其左子树中的任意结点的键而小于右子树中的任意结点的键

删除最小结点

  • 找到最小结点（不停查询左子结点直到找到左子结点为空的结点，即为最小结点）
  • （如果有右子结点）将最小结点的父节点的左子结点，更新为最小结点的右结点

删除任意结点

  • 找到要被删除的结点t
  • 找到t右子树中的最小结点x，x即为t的后继结点，会由x替代t的位置
  • 在t的右子树中执行“删除最小结点”操作，即删除x；同时将x的右子树更新为t的右子树
  • 将x的左子树更新为t的左子树

平衡查找树 - Balanced Search Trees

普通的二叉查找树的效率很大程度上依赖输入的随机性，如果输入不够随机，其效率会大幅下降；其核心原因是，不够随机的输入会让生成的树严重“失衡”

而一些实现可以通过一些手段调整查找树的结构，从而让最后形成的查找树更加平衡，并且不被输入掣肘

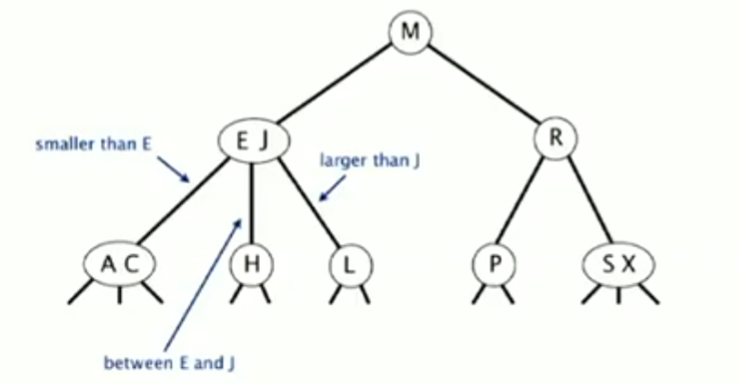
2-3查找树 - 2-3 Tree

2-3查找树允许部分结点存储两个键，其由以下两种结点构成

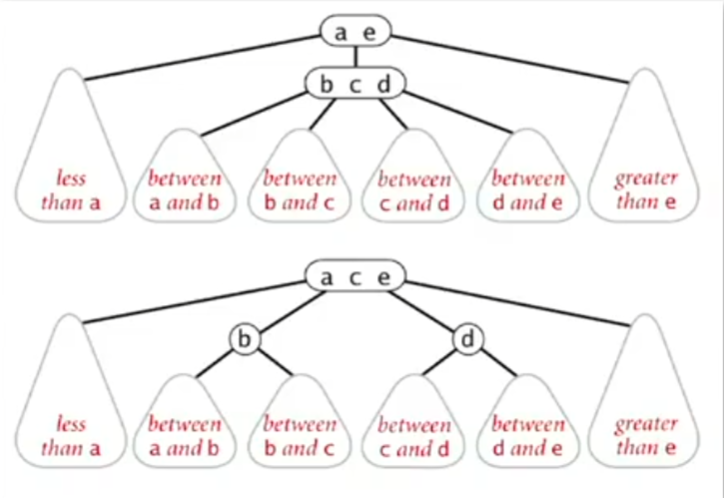
  • 2-结点：一个键、两个子结点（<key、>key）
  • 3-结点：两个键、三个子结点（<key1、>key1 & <key2、>key2）

2-3会始终保持完美平衡（始终是满二叉树）

image-20250405024533495

在查找操作上，2-3树并没有什么特殊的，就像普通的二叉查找树一样操作即可

而在插入操作上，2-3树便有些门道了

首先依据插入元素大小查找到最后，此时依据最后的结点类型分为两种情况

如果是2-结点

  • 让元素直接加入这个2-结点，使其变为一个3-结点

如果是3-结点

  • 先让元素加入，使其变为一个4-结点（含有三个键）
  • 分裂4-结点，让中间键加入其父节点，剩余两个键分别成为一个2-结点
  • 如果父节点已经是一个3-结点了，重复上述分裂的步骤

在2-3树中，只有根节点变为4-结点，发生“分裂时，树的高度才会增长；和普通的二叉查找树不同，2-3树的生长是由下向上的

image-20250405030405424

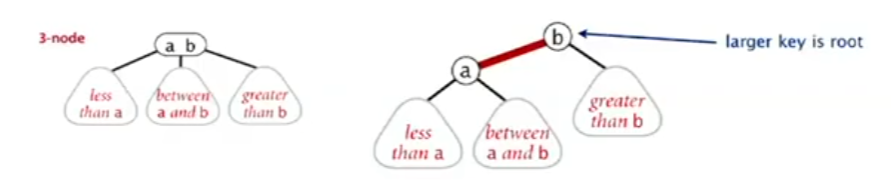
红黑树 - red-black BSTs

红黑树是一种使用二叉树来表示2-3树的方式，我们将3-结点拆开；

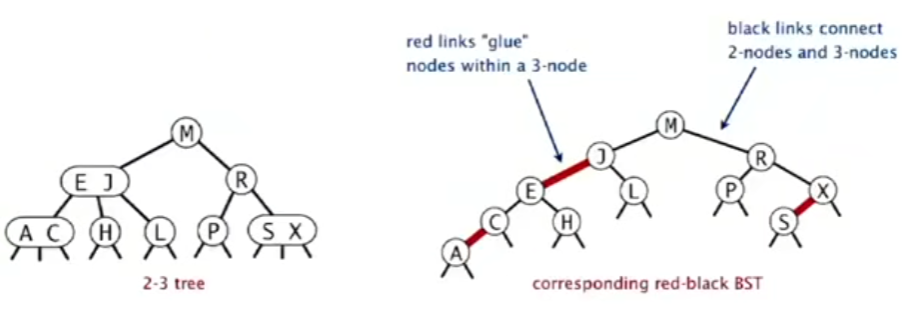
在左倾红黑树中，在构成3-结点时，我们使用左倾的链接来表示3-结点；同时，我们将用于链接原3-结点的两个键的链接成为红色的链接，其他则为黑色，这样我们便可以知道哪些是原先的3-结点

image-20250412231807209

通过这种方式，任意的2-3树都可以被表示为二叉树

image-20250412232204524

左倾红黑树的性质

  • 没有节点与两个红色连接相连
  • 从树根到叶子节点经过的黑色连接数量都相同（2-3树是完全平衡的）
  • 红色连接总是左倾

查找

在红黑树中进行搜索和在一般的二叉搜索树完全相同，我们不需要考虑颜色的问题

红黑树的优势也正在于其在不需要改变二叉树结构的情况下实现了二叉搜索树的相对平衡

我们基于二叉搜索树结构编写的算法可以在完全不改变的情况下应用与红黑树

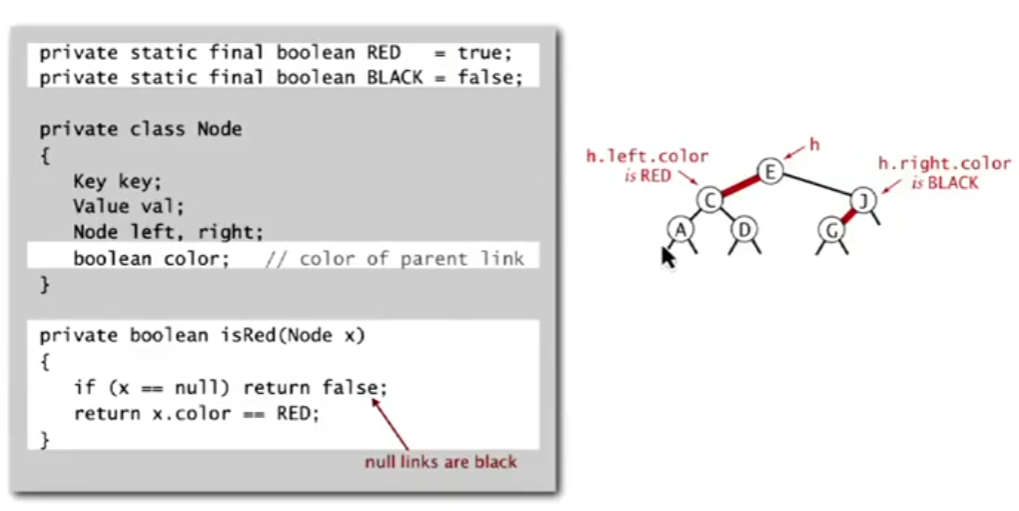
颜色的表示

在实际代码的编写中，我们往往并不会显示地构建“连接”这一结构

因为在二叉树中一个结点只会被一个其他结点引用，所以我们可以把连接的颜色存储在结点中

image-20250412233158461

在上面的实例中，E-C直接是红色，所以我们可以将红色存在C结点中；

同时，我们默认所有所有空结点都是黑色

三种基本操作

  • 左旋：接收一个右倾的红色连接，将其转回左倾
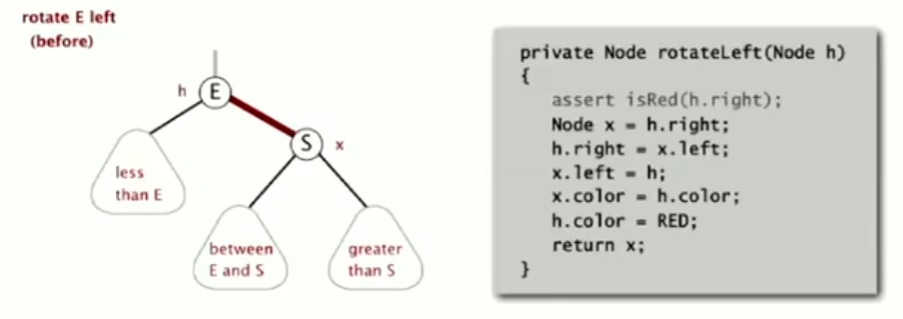
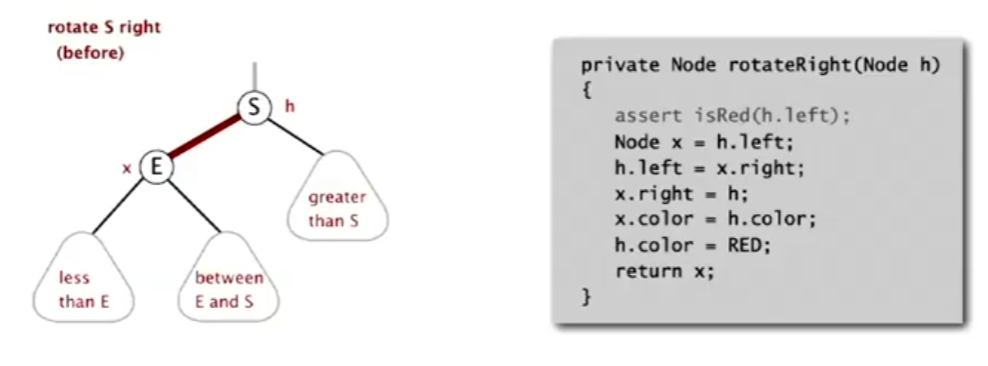
image-20250412233830881
  • 右旋：和左旋同理，即使在一个左倾红黑树中，我们有时也需要暂时地让树的部分变为右倾
image-20250412234343569

需要注意的是，左旋右旋都没有改变结点的相对大小关系，也没有破坏黑色平衡，这只是一种调整手段

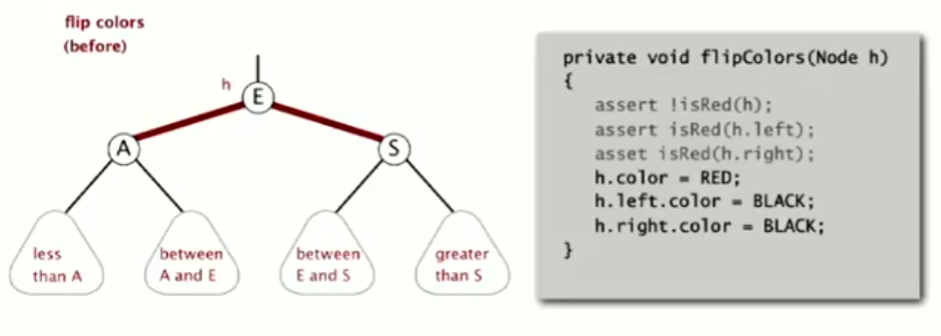
  • 颜色翻转：这是模拟2-3树的生长过程的操作，（我们会暂时构建出一个4-结点，然后再将其分裂），在红黑树中，我们只需要改变颜色即可
image-20250412234823024

将E-A、E-S改为黑的操作实现了分裂，而将E改为红则体现了将E加入其父节点的生长过程

插入

我们实现插入的基本策略便是去使用上述的三种基本操作模拟我们在2-3树中干的事情

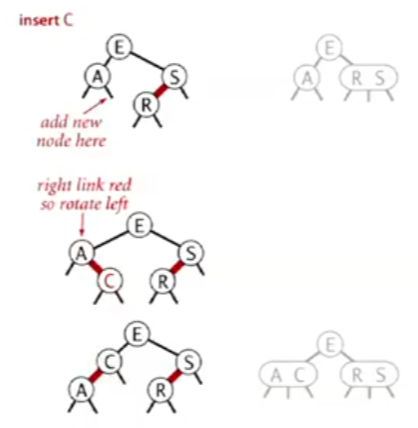
image-20250412235328263

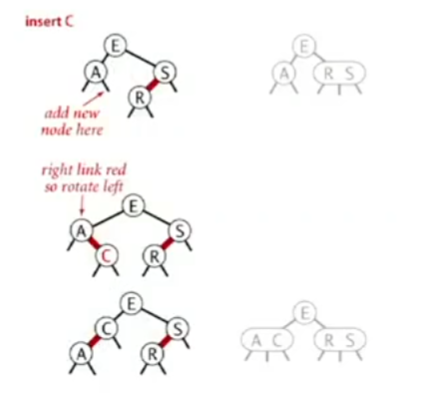
  1. 插入结点至树底部的2-结点

    • 进行标准的BST插入，将新连接（结点）的颜色设置为红

    • 如果红连接右倾，这将其左旋

image-20250522180109558

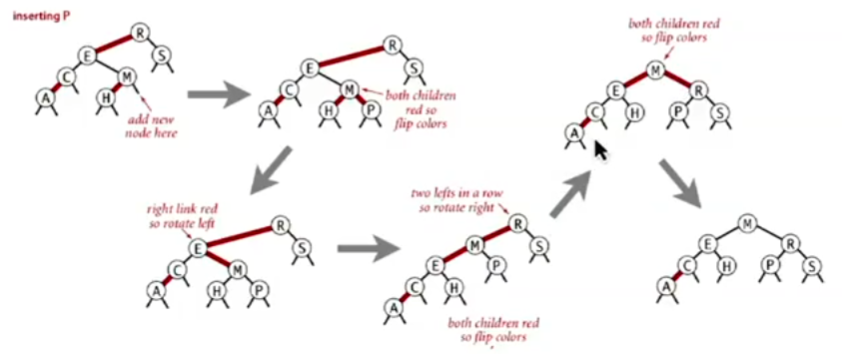
  1. 插入结点至树底部的3-结点

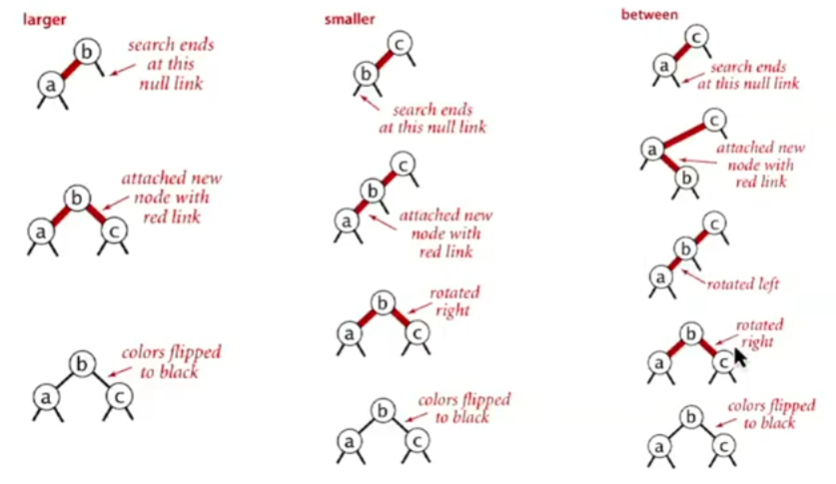
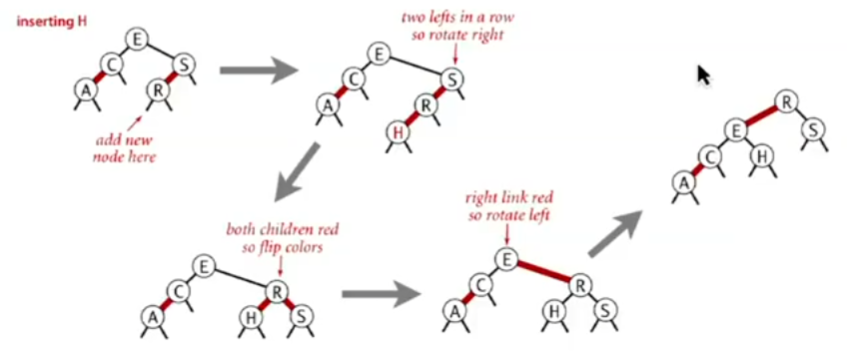
    • 进行标准的BST插入，将新连接（结点）的颜色设置为红
    • （如果构成的4-结点不平衡）旋转以平衡4-结点
    • 进行4-结点的颜色翻转，将红色向上传递
    • （如果右倾）旋转使其左倾
    image-20250522181634575

    下面是向一个只有两个结点的树插入一个结点的分类讨论，上面的流程很大程度上是从下面的分类讨论中总结出来的

image-20250522181128007
  1. （如果树不符合要求）重复case1或case2，在实现上会使用递归的方式实现
image-20250522181935783

C++简单实现

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
template<Comparable KEY, typename VALUE>
class RedBlackBST {
private:
    struct Node {
        KEY key;
        VALUE value;
        Node *left;
        Node *right;
        bool is_red;

        Node(KEY k, VALUE v, bool red = true)
            : key(k), value(v), left(nullptr), right(nullptr), is_red(red) {}
    };

    Node *root_ = nullptr;

    bool is_red(Node *node) const {
        if (node == nullptr) return false;
        return node->is_red;
    }

    Node* rotateLeft(Node *h) {
        assert(h != nullptr && is_red(h->right));
        Node* x = h->right;
        h->right = x->left;
        x->left = h;
        x->is_red = h->is_red;
        h->is_red = true;
        return x;
    }

    Node* rotateRight(Node *h) {
        assert(h != nullptr && is_red(h->left));
        Node* x = h->left;
        h->left = x->right;
        x->right = h;
        x->is_red = h->is_red;
        h->is_red = true;
        return x;
    }

    void flipColor(Node *h) {
        assert(h != nullptr && h->left != nullptr && h->right != nullptr);
        assert(!is_red(h) && is_red(h->left) && is_red(h->right));
        h->is_red = true;
        h->left->is_red = false;
        h->right->is_red = false;
    }

    Node* put(Node *h, KEY key, VALUE value) {
        if (h == nullptr) return new Node(key, value, true);

        if (key < h->key)        h->left = put(h->left, key, value);
        else if (key > h->key)    h->right = put(h->right, key, value);
        else                    h->value = value;

        if (is_red(h->right) && !is_red(h->left))         h = rotateLeft(h);
        if (is_red(h->left) && is_red(h->left->left))     h = rotateRight(h);
        if (is_red(h->left) && is_red(h->right))         flipColor(h);

        return h;
    }

    const Node* get(Node *h, const KEY& key) const {
        while (h != nullptr) {
            if (key < h->key)        h = h->left;
            else if (key > h->key)    h = h->right;
            else                    return h;
        }
        return nullptr;
    }

public:
    bool is_empty() const {
        return root_ == nullptr;
    }

    void put(KEY key, VALUE value) {
        root_ = put(root_, key, value);
        root_->is_red = false;
    }

    std::optional<VALUE> get(const KEY& key) const {
        const Node* res = get(root_, key);
        if (res == nullptr) return std::nullopt;
        return res->value;
    }
};