img

Lecture 01 Overview of Computer Graphics

Computer Graphics is AWESOME

课程主题 Course Topics：

  • 光栅化 Rasterization
  • 曲线与曲面 Curves and Meshes
  • 光线追踪 Ray Tracing
  • 动画与模拟 Animation / Simulation

光栅化 Rasterization

把三维空间的几何形体显示在屏幕上

实时渲染：>30FPS 每秒生成30张以上的图片；否则为离线渲染

曲线与曲面 Curves and Meshes

如何表现曲线与曲面

光线追踪 Ray Tracing

从相机中发射光线穿过每个像素来获取极尽真实的画面效果

动画与模拟 Animation / Simulation

布料模拟、弹性模拟等物理模拟

GAMES101是什么

We learn Graphics, not Graphics API

不教OpenGL / DirectX / Vulkan

Lecture 02 Review of Linear Algebra

点积 Dot Product

a⃗⋅b⃗=∣a⃗∣∣b⃗∣cos⁡θa⃗⋅b⃗=(xaya)⋅(xbyb)=xaxa+yayb\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}| \cos \theta \newline \vec{a}\cdot\vec{b}=\binom{x_a}{y_a}\cdot\binom{x_b}{y_b}=x_ax_a+y_ay_b

  • 找到两个向量之间的夹角：由点积除以两个向量的模即可得到向量夹角的余弦值
  • 找到向量的投影：由一个向量的模乘以夹角余弦值即可得到投影的长度，从而可以进行向量的分解
  • 得到向量是否接近
  • 得到向量的方向性

叉积 Cross Product

∣a⃗×b⃗∣=∣a⃗∣∣b⃗∣sin⁡θa⃗×b⃗=−b⃗×a⃗|\vec{a} \times \vec{b}| = |\vec{a}||\vec{b}|\sin \theta \newline \vec{a} \times \vec{b} = -\vec{b} \times \vec{a}

  • 判断向量的左右
  • 判断向量的内外

给定一个点P，要求判断其是否在三角形ABC内部

若AB→×AP→、BC→×BP→、CA→×CP→\overrightarrow{AB} \times \overrightarrow{AP}、\overrightarrow{BC} \times \overrightarrow{BP}、\overrightarrow{CA} \times \overrightarrow{CP}​三个叉乘所得的符号相同，则P在ABC内部

  • 建立正交坐标系

矩阵 Matrices

矩阵乘法：(M×N)(N×P)=(M×P)(M\times N)(N\times P)=(M\times P)才能乘​

没有交换律 Non-commutative

Lecture 03 Transformation

二维变换

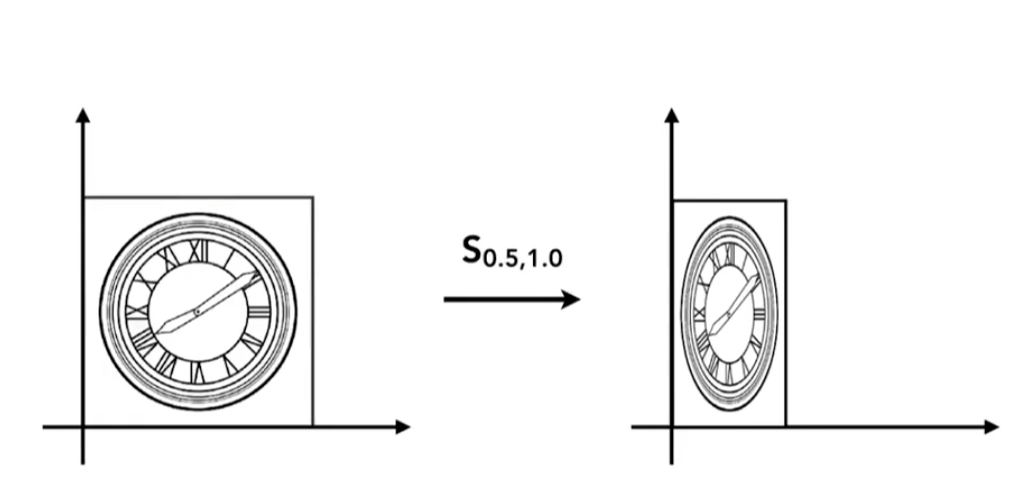
  • 缩放矩阵 Scale Matrix
image-20240309214631581

[x′y′]=[sx00sy][xy]\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s_{x} & 0 \\ 0 & s_{y} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}

  • 反射矩阵 Reflection Matrix
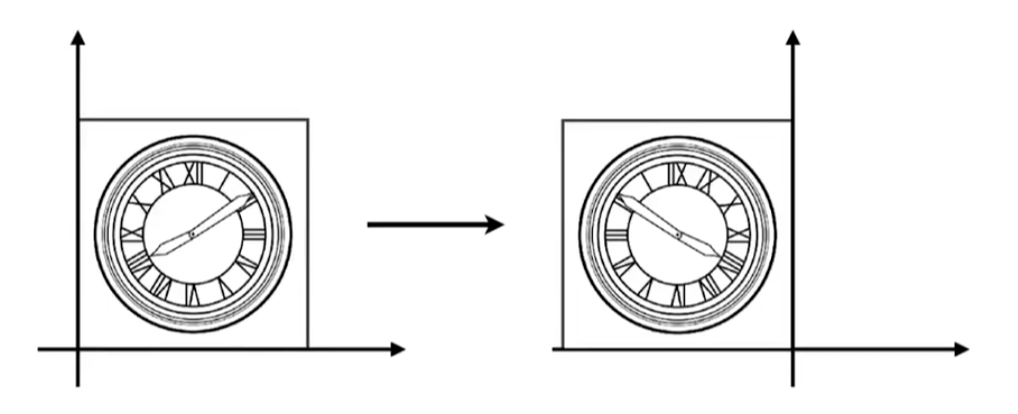
image-20240309214700369

[x′y′]=[−1001][xy]\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}

  • 错切矩阵 Shear Matrix
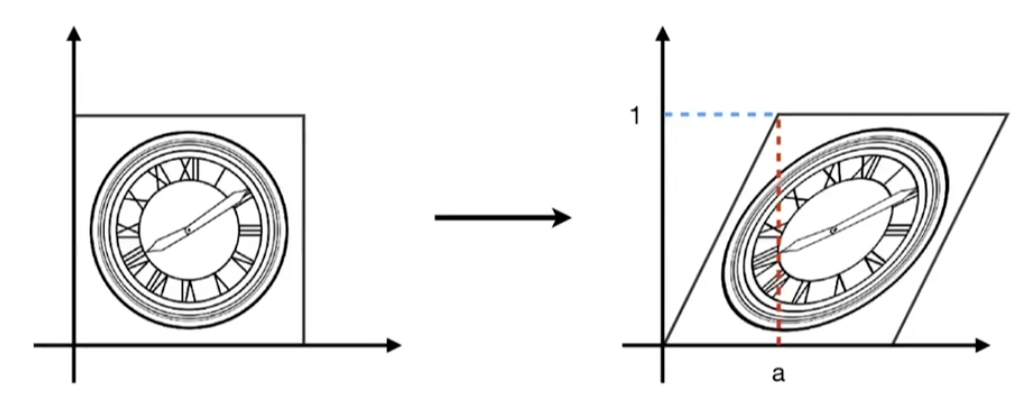
image-20240309214715015

[x′y′]=[1a01][xy]\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}

  • 旋转矩阵 Rotation Matrix
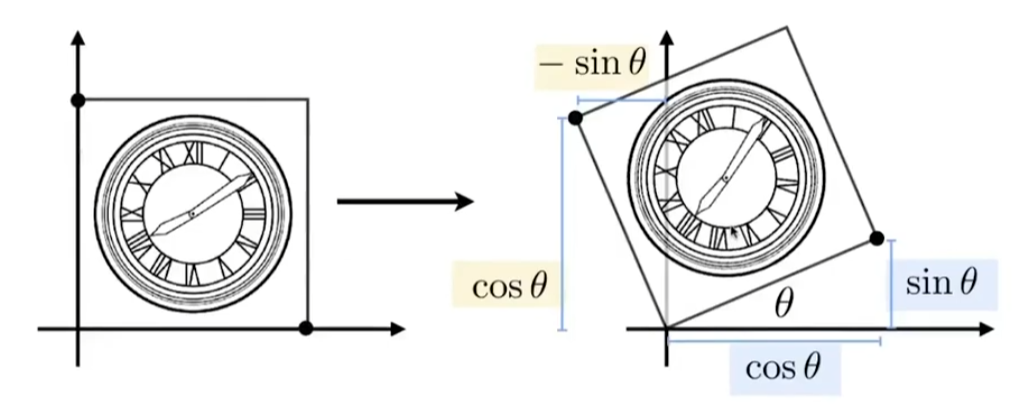
image-20240309214808366

默认逆时针沿原点旋转

[x′y′]=[cos⁡θ−sin⁡θsin⁡θcos⁡θ][xy]\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}

线性变换：x′=Mxx'=Mx

齐次坐标 Homogeneous Coordinate

为什么我们需要齐次坐标

平移变换不能用矩阵变换的形式表示出来

[x′y′]=[abcd][xy]+[txty]\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_{x} \\ t_{y} \end{bmatrix}

这并不是一个线性变换

但是我们不希望让平移变换变成一个特殊情况

齐次坐标的引入可以表示这点

解决方法：齐次坐标

[x′y′w′]=[10tx01ty001][xy1]=[x+txy+ty1]\begin{bmatrix} x' \\ y' \\ w' \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x + t_{x} \\ y + t_{y} \\ 1 \end{bmatrix}

通过增加一个维度可以将平移也写成矩阵相乘的形式

  • 2D point = (x,y,1)T(x,y,1)^T
  • 2D vector = (x,y,0)T(x,y,0)^T

仿射变换 Affine Transformations

仿射变换是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间

仿射变换可以通过齐次坐标的形式转换为一次线性变换

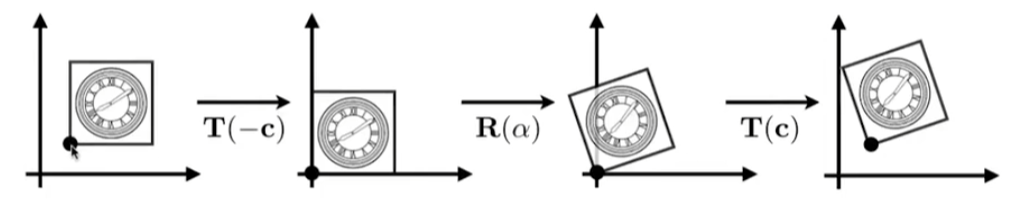
变换的组合 Composing Transforms

  • 复杂的变换可以由多个简单的变换组合而成
  • 变换的顺序很重要

变换的分解 Decomposing Complex Transforms

image-20240309221700197

三维变换

  • 3D point = (x,y,z,1)T(x,y,z,1)^T
  • 3D vector = (x,y,z,0)T(x,y,z,0)^T

仿射变换先变换再平移

旋转矩阵是正交矩阵，即其转置矩阵是其逆矩阵

Lecture 04 Transformation Cont.

三维变换 3D Transformation

  • Scale

S(sx,sy,sz)=[sx0000sy0000sz00001]S(s_{x},s_{y},s_{z}) = \begin{bmatrix} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

  • Translation

T(tx,ty,tz)=[100tx010ty001tz0001]T(t_{x},t_{y},t_{z}) = \begin{bmatrix} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix}

  • Rotate

Rx(α)=[10000cos⁡α−sin⁡α00sin⁡αcos⁡α00001]Ry(α)=[cos⁡α0sin⁡α00100−sin⁡α0cos⁡α00001]Rz(α)=[cos⁡α−sin⁡α00sin⁡αcos⁡α0000100001]Rxyz(α,β,γ)=Rx(α)Ry(β)Rz(γ)R_{x}(\alpha) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha & 0 \\ 0 & \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \newline R_{y}(\alpha) = \begin{bmatrix} \cos\alpha & 0 & \sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\alpha & 0 & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \newline R_{z}(\alpha) = \begin{bmatrix} \cos\alpha & -\sin\alpha & 0 & 0 \\ \sin\alpha & \cos\alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \newline R_{xyz}(\alpha,\beta,\gamma)=R_{x}(\alpha)R_{y}(\beta)R_{z}(\gamma)

上面的变换形式被称为欧拉角

其常被用于飞行模拟中：滚转roll, 俯仰pitch, 偏航yaw

罗德里格斯旋转公式

四元数(quaternion)可以Lerp

观测变换 Viewing Transformation

MVP变换：模型（model），视图（view），投影（projection）

视图变换 View/Camera Transformation

定义相机

  • Position e⃗\vec{e}
  • Look-at / gaze direction g^\hat{g}
  • Up direction t^\hat{t}

相机拍摄的是相对运动，那么为何不让相机固定住呢

  • 相机永远在原点，永远以Y轴为向上，相机永远看向-Z方向（约定俗成）
  • 其他物体的运动都是相对相机的运动

将相机变换到上述固定位置

Mview=RviewTview设相机原点在e⃗，看向g^，t^为上e⃗平移至原点：Tview=[100−xe010−ye001−ze0001]g^旋转至−Z，t^旋转至Y，(g^×t^)旋转至X这样的旋转矩阵很难写，但其逆矩阵很简单，因为旋转矩阵是正交矩阵，写出其逆矩阵后转置即可得到要求的矩阵Rview−1=[xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001]→Rview=[xg^×t^yg^×t^zg^×t^0xtytzt0x−gy−gz−g00001]M_{view}=R{view}T{view} \\ \\ 设相机原点在\vec{e}，看向\hat{g}，\hat{t}为上 \\ \\ \vec{e}平移至原点： T_{view}= \begin{bmatrix} 1 & 0 & 0 & -x_{e} \\ 0 & 1 & 0 & -y_{e} \\ 0 & 0 & 1 & -z_{e} \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ \\ \hat{g}旋转至-Z，\hat{t}旋转至Y，(\hat{g}\times\hat{t})旋转至X \\ 这样的旋转矩阵很难写，但其逆矩阵很简单，因为旋转矩阵是正交矩阵，写出其逆矩阵后转置即可得到要求的矩阵 \\ \\ R_{view}^{-1}= \begin{bmatrix} x_{\hat{g}\times\hat{t}} & x_{t} & x_{-g} & 0 \\ y_{\hat{g}\times\hat{t}} & y_{t} & y_{-g} & 0 \\ z_{\hat{g}\times\hat{t}} & z_{t} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \to R_{view}= \begin{bmatrix} x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & 0 \\ x_{t} & y_{t} & z_{t} & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

视图变换和模型变换常常被一起提到，模型和相机常常一起变换，称为模型视图变换

投影变换 Projection Transformation

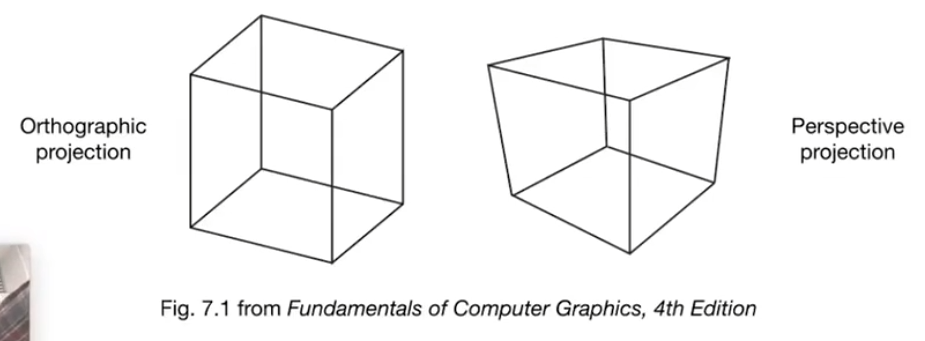
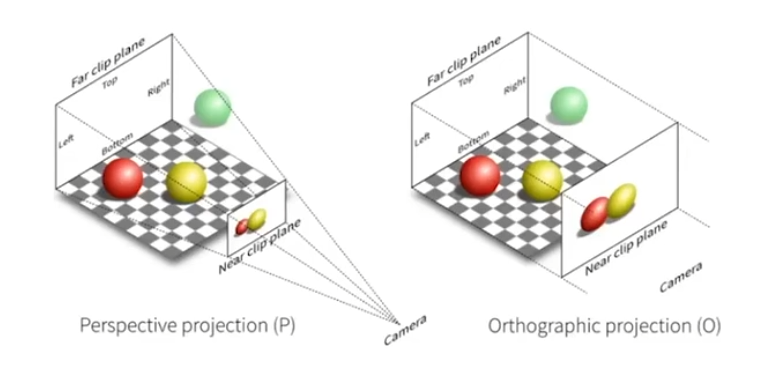
image-20240309234448916 image-20240309234548442

正交投影不会有近大远小

正交投影 Orthographic Projection

一个易于理解的方法：

  • 把相机放到原点上，向-Z方向看，Y为上
  • 扔掉Z坐标
  • 平移缩放得到的结果到[−1,1]2[-1,1]^{2}​（约定俗成）

正式的做法：

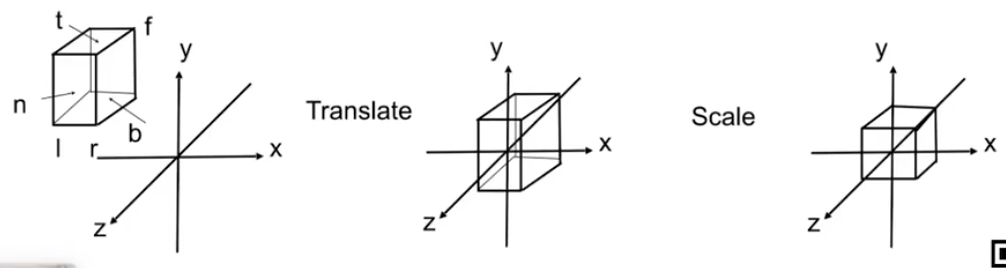
image-20240309234954407
  • 把一个立方体变换为正则(canonical)立方体：平移，缩放

Mortho=[2r−l00002t−b00002n−f00001][100−r+l2010−t+b2001−n+f20001]M_{ortho}= \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix}

透视投影 Perspective Projection

  • 首先挤压四椎体使其称为一个立方体
  • 进行正交投影

近平面点不变，远平面z不变

f1a9a8eafe39abf782f7389e2838cf4

Lecture 05 Rasterization 1 (Triangles)

视场角（FOV-Field of View）和宽高比（Aspect Ratio）与视锥各参数的转化

image-20240312205336381

从正则立方体到屏幕空间

通过在变换中推导出的MVP矩阵，我们可以将所有物体压缩进正则立方体中，而下一步便是将这些东西放到屏幕上了

屏幕 Screen

  • 一个二维的像素数组
  • 数组的大小：分辨率（resolution）
  • 一种典型的光栅（raster）成像设备

光栅（Raster）就是屏幕（Screen）的德语，光栅化（Rastize）就是将物体显示在屏幕上

屏幕空间

image-20240312210102675
  • 像素通过(x,y)(x, y)的坐标形式表示，像素的中心在(x+0.5,y+0.5)(x+0.5, y+0.5)
  • 如果我们认为屏幕的分辨率为width∗heightwidth*height，那么共有(0,0)(0, 0)~(width−1,height−1)(width-1, height-1) 个像素
  • 屏幕空间覆盖了(0,0)(0, 0)到(width,height)(width, height)的范围

视口变换

  • 与z轴无关
  • 由[−1,1]2[-1,1]^2到[0,width]×[0,height][0,width]\times[0,height]

Mviewport=[width200width20height20height200100001]M_{viewport}= \begin{bmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \\ 0 & \frac{height}{2} & 0 & \frac{height}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

三角形

为什么是三角形

  • 三角形是最基础的多边形
  • 可以用三角形来表示其他多边形
  • 内部一定是平面的
  • 内外定义非常清楚
  • 方便进行内部差值

采样 Sampling

这是最简单的光栅化方法

把一个函数离散化：给定一个函数，得到一个个具体的值

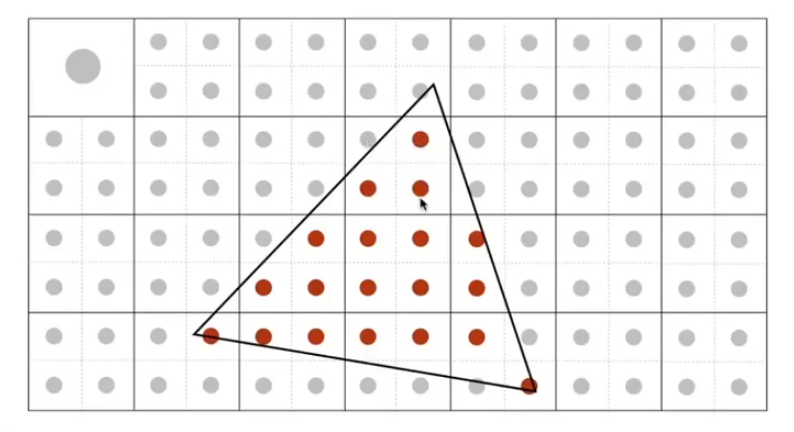
采样一个像素的中心是否在三角形内部

inside(t,x,y)={1(x,y) in △t0otherwiseinside(t,x,y)= \begin{cases} 1 \quad (x,y)\ in\ \triangle t\\ 0 \quad otherwise \end{cases}

  • 通过三次叉积即可判断点是否在三角形内部

  • 边界问题：要么不做处理，要么特殊处理，自洽即可

  • 通过三角形的包围盒（Bounding Box）提高采样效率：只要在包围盒内的像素才有可能被覆盖到

image-20240312214834322
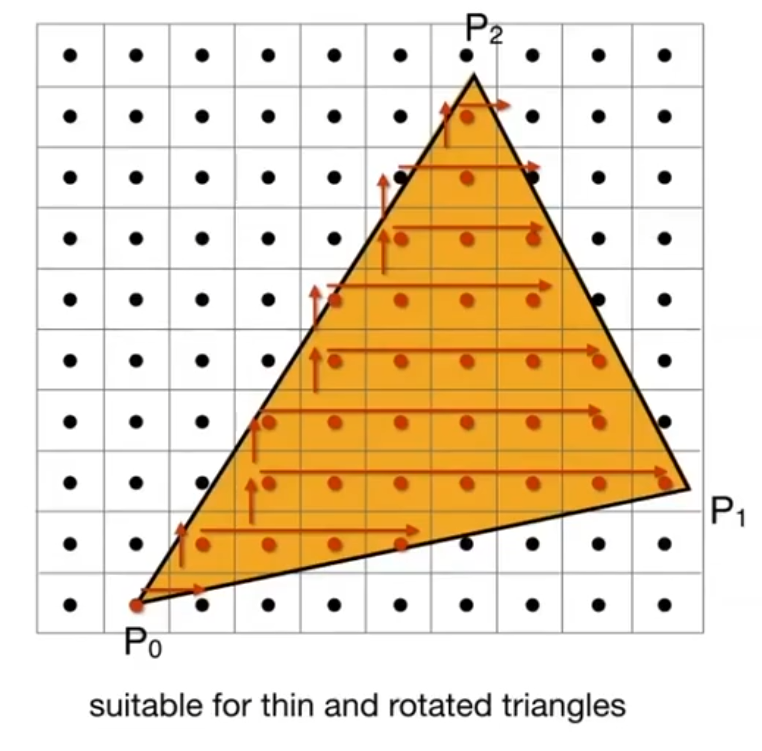
  • 还有很多加速光栅化的方式：如下面的只从三角形每行的第一个像素开始
image-20240312215039137

光栅化图形学的严重问题：抗锯齿（Jaggies）与反走样（Aliasing）

Lecture 06 Rasterization 2 (Antialiasing and Z-Buffering)

采样（sample）在计算机图形学中无处不在

  • 光栅化是一种对2D像素点的采样
  • 摄影是一种对感光元件的采样
  • 视频是一种对时间的采样

采样会产生一系列Sample Artifacts（瑕疵）

  • 锯齿 Jaggies

  • 摩尔纹 Moire Pattern

  • Wagon wheel effect（False Motion）

在走样的背后：信号变化太快，但采样频率太慢

反走样采样（Antialiased Sampling）

image-20240320082236039 image-20240320082428051

走样Alias：同样采样方法采样两个不一样的函数，得到的结果我们无法区分

滤波Filtering：去掉一系列特定频率

高通滤波：去掉低频信号 - 锐化、剩余边界

低通滤波：去掉高频信号 - 模糊

  • 滤波Filtering = 卷积convolution

  • 时域上的卷积 = 频域上的乘积

  • 从频率上说：采样Sampling = 重复Repeating

如何减少走样问题

  • 增加采样率
  • 反走样：先模糊（低通滤波）再采样
image-20240321233214688

Antialiasing By Supersampling

MSAA - Multisample Anti-Aliasing

使用更多的采样点近似地改善走样 - 信号的模糊

image-20240321233735273

代价：增加了计算量

FXAA - Fast Approximate Anti-Aliasing

图像的后期处理 - 替换有锯齿的边界

和采样本身无关

TAA - Temporal Anti-Aliasing

把MSAA增加的采样点分布在时间维度上

帧与帧之间采样点不同，通过与上一帧的比较进行反走样

超分辨率 Super Resolution

  • 超分辨率是将低分辨率映射至高分辨率时进行的画面优化
  • 某种程度上和反走样异曲同工，本质相同
  • DLSS (Deep Learning Super Sampling)

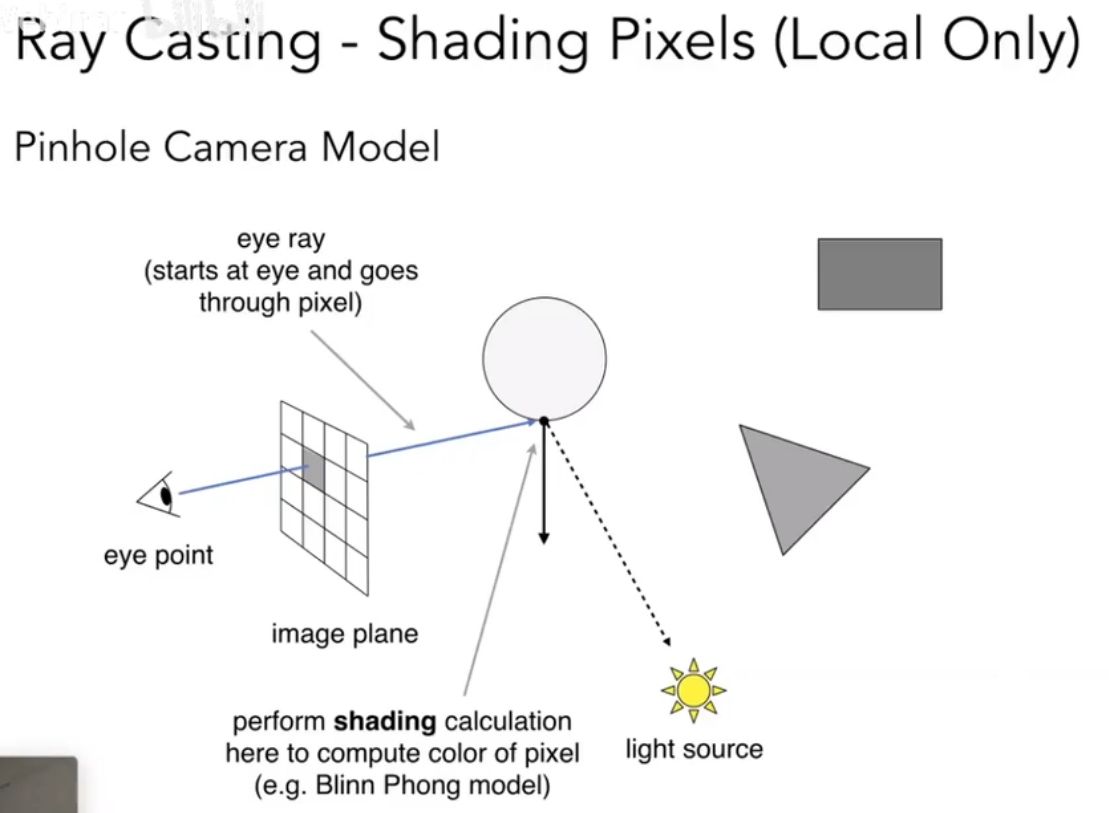
Lecture 07 Shading 1 (Illumination, Shading and Graphics Pipeline)

画家算法 Painter’s Algorithm

类似油画的算法：先画远处的，后画的会覆盖先画的

  • 需要进行深度排序，对于nn个三角形需要O(nlogn)O(nlogn)

  • 在处理类似下面的情况会发生问题

image-20240324213827464

Z-Buffer

  • 对每个像素记录当前的最小z值
  • 需要一个额外的Buffer记录深度值：Frame Buffer记录颜色值，Depth Buffer记录深度值
image-20240324214127685

Algorithm

  • 将所有的深度值初始化为∞\infin

  • 在光栅化时：

1
2
3
4
5
6
7
8
9
10
11
for (each trangle T) {
    for (each sample(x, y, z) in T) {
        if (z < depthBuffer[x, y]) {
            frameBuffer[x, y] = rgb;
            depthBuffer[x, y] = z;
        }
        else {
            ...
        }
    }
}

  • Complexity：O(n)O(n)

  • 和计算顺序无关

着色 Shading

着色：向物体应用材质的过程

一个简单的着色模型：Blinn-Phong Reflectance Model

image-20240324220557877
  • View direction - v
  • Surface normal - n
  • Light direction - l
  • Surface parameters - colors, shininess…

Shading is Local: shading ≠ shadow

漫反射 Diffuse Reflection

  • 光线会均匀地散射向各个方向
image-20240324220949796 image-20240324221351392
  • 需要考虑接收到光的能量：Lambert’s cosine law，cosθ=l∗ncos\theta = l *n
image-20240324221643233 image-20240324221723383

公式：

Ld=kd(I/r2)max(0,n∗l)L_d = k_d(I/r^2)max(0,n \ast l)

Lecture 08 Shading 2 (Shading, Pipeline and Texture Mapping)

镜面反射项 Specular Term (Blinn-Phong)

当观察向量和反射向量足够接近时，就会出现高光现象

Blinn-Phong模型：当观察向量和反射向量很接近时，就说明半程向量（half vector）和法线很接近

image-20240325225419328

Blinn-Phong简化了被吸收的光，省略了max(0,n∗l)max(0, n\ast l)​

Ls=ks(I/r2)max(0,cos⁡α)p=ks(I/r2)max(0,n∗h)p\begin{aligned} L_s & = k_s(I/r^2)max(0,\cos\alpha)^p \\ & = k_s(I/r^2)max(0,n\ast h)^p \end{aligned}

为什么会有p次方：直接用cos函数的容忍度太高了，如下图所示，一般Blinn-Phong模型中p取100~200

image-20240325225858065

环境光照项 Ambient Term

真实的环境光极度复杂，很难直接进行模拟

在这里直接假设所有物体收到的环境光永远都是相同的

La=kaIaL_a = k_a I_a

这是一个估值、一个假设

image-20240325230543165

环境光和观察角度、入射角度、法线都无关，其是一个常数

Blinn-Phong反射模型

L=La+Ld+Ls=kaIa+kd(I/r2)max(0,n∗l)+ks(I/r2)max(0,n∗h)p\begin{aligned} L & = L_a + L_d + L_s \\ & = k_a I_a + k_d(I/r^2)max(0,n \ast l) + k_s(I/r^2)max(0,n\ast h)^p \end{aligned}

image-20240325231149673

着色频率 Shading Frequencies

image-20240325231345179

这三个球的几何表示其实完全相同，只是着色频率的区别

三个球分别对应：对平面着色、对顶点着色（使用差值计算内部颜色）、对像素（使用差值计算内部法线）着色

平面着色 Shade each triangle (flat shading)

  • 三角形是一个面，有一条法线
  • 对光滑平面来说效果并不好

高洛德着色 Shade each vertex (Gouraud shading)

  • 通过顶点差值计算像素的颜色
  • 每个顶点有一条法线

古罗着色 Shade each pixel (Phong shading)

  • 通过顶点差值计算像素的法线
  • 为每个像素应用着色模型

着色方法的比较

image-20240325232509091

当模型面数很高时，简单的着色模型效果也会不错

顶点/像素法线的计算

  • 顶点法线：顶点周围面的法线的平均（普通或加权）

通过顶点法线差值计算像素法线

图形（实时渲染）管线 Graphics (Real-time Rendering) Pipeline

管线：如何从场景到图

image-20240325233137272 image-20240325233721974

Shader Programs

  • 编写顶点和片元的处理策略
  • 描述一个单一顶点或片元的操作（会应用到所有顶点/片元上）

纹理映射 Texture Mapping

定义任何一个点的属性

任何一个三维物体的表面其实是二维的，纹理就是三维物体表面再开后的二维面

模型上的每个三角形顶点都会被分配给纹理上的一个坐标（u,v）

image-20240325235251522

纹理可以被多次映射

image-20240325235422215

Lecture 09 Shading 3 (Texture Mapping Cont.)

在三角形内部进行插值：重心坐标 Barycentric Cooridnates

定义

image-20240326215604537

重心坐标是定义在某一三角形上的

给定任意一个三角形，其平面上任意点的坐标都可以表示为其顶点坐标的线性组合

(x,y)=αA+βB+γCα+β+γ=1(x,y) = \alpha A + \beta B + \gamma C \\ \alpha + \beta + \gamma = 1

对于坐标(x,y)(x,y)，(α,β,γ)(\alpha,\beta,\gamma)便是其重心坐标

而对于三角形内部的点，α>0且β>0且γ>0\alpha>0且\beta>0且\gamma>0

image-20240326220337674

而α、β、γ\alpha、\beta、\gamma的值可以通过面积比得到

由上述推导可得，三角形的重心的重心坐标为(13,13,13)(\frac{1}{3},\frac{1}{3},\frac{1}{3})

应用

我们可以用重心坐标得到三角形内部任意点的插值

image-20240326220755100

重心坐标虽好用，但是其不能保证在投影后重心坐标不变，我们理论上不应该对投影后的三角形应用重心坐标进行插值，我们应该使用逆变换得到其原来的三维坐标，再对三维坐标进行计算

应用纹理

我们可以通过采样得到采样点/屏幕坐标计算得到其对应的uv值，然后根据uv值从纹理上得到对应的颜色，之后通过光照反射模型（比如Blinn-Phong）将颜色应用到反射系数上了

但是这样会带来一些问题：

纹理放大 Texture Magnification

如果纹理太小了

如果纹理很小但是分辨率很高，纹理就会被拉大

image-20240326221920235

我们可以通过简单的四舍五入找最佳的点来解决这一点，这样一个texel就会被映射到多个临近pixel上，但这会带来很多锯齿

一些方法可以改善这一问题

  • 双线性插值 Bilinear Interpolation
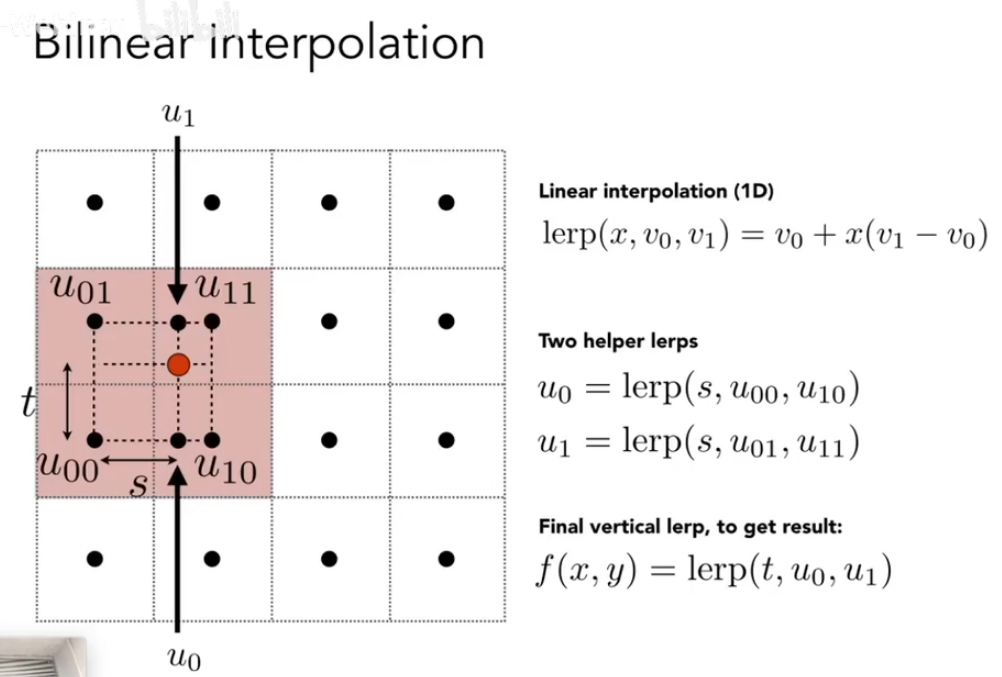
image-20240326222613903
  • 双三次插值 Bicubic Interpolation

开销更大，效果更好

如果纹理太大了

image-20240326223554785

每个像素覆盖的texel数量不同，有的像素覆盖了过多的texel

超采样可以一定程度解决这个问题，但是这开销太高了

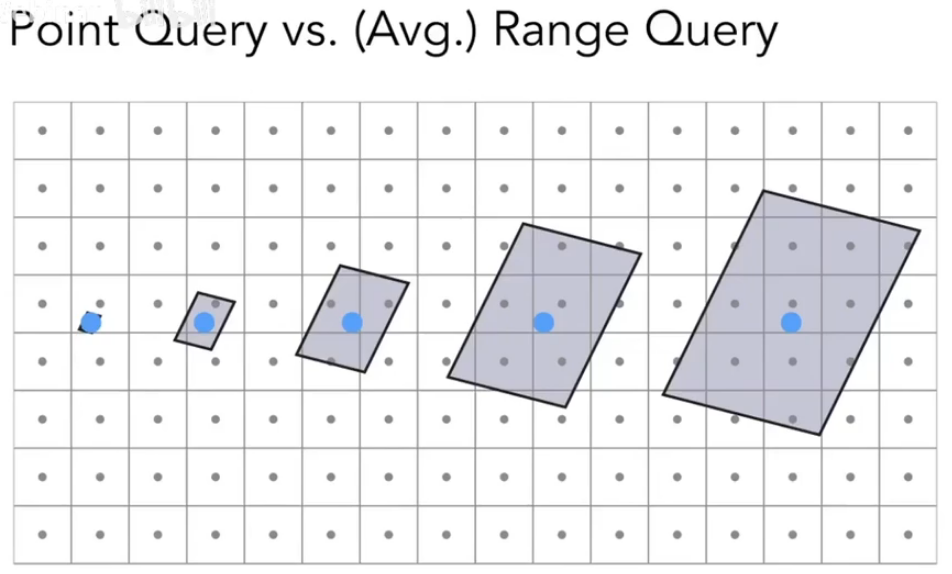
image-20240326224000188

范围查询

Mipmap：允许进行范围查询（快速，近似，正方形）

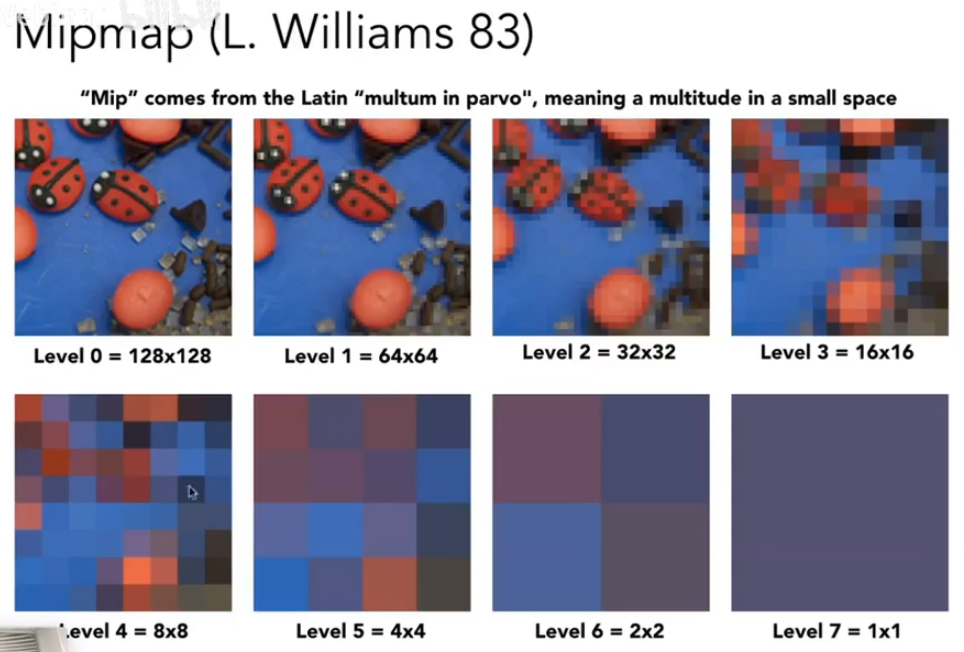
image-20240326224136187 image-20240326224907408

三线性插值

image-20240326225258233

Mipmap可能让远处的细节糊掉：Overblur

一个方法可以一定程度改善这一问题：各向异性过滤 Anisotropic Filtering

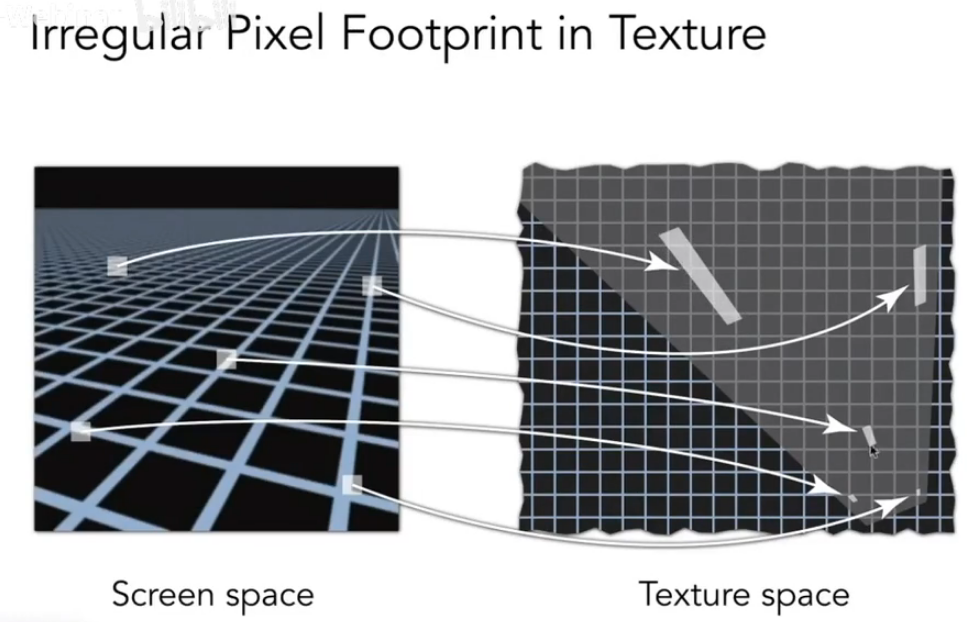
image-20240326225758529 image-20240326225814755

各向异性过滤会将图片按长宽分别进行压缩从而得以支持矩形的范围查询，改善了Mipmap只支持正方形的问题

其可以一定程度上解决问题，但是对于一些非常难搞的情况，比如实际的映射范围是斜着的，其仍然存在走样的情况

因此人们还发明了一些其他方法：EWA - 通过将范围转变为圆形进行多次查询

image-20240326230142240

纹理的广泛作用

纹理本质上可以被理解为一块可以进行查询的内存（数据）

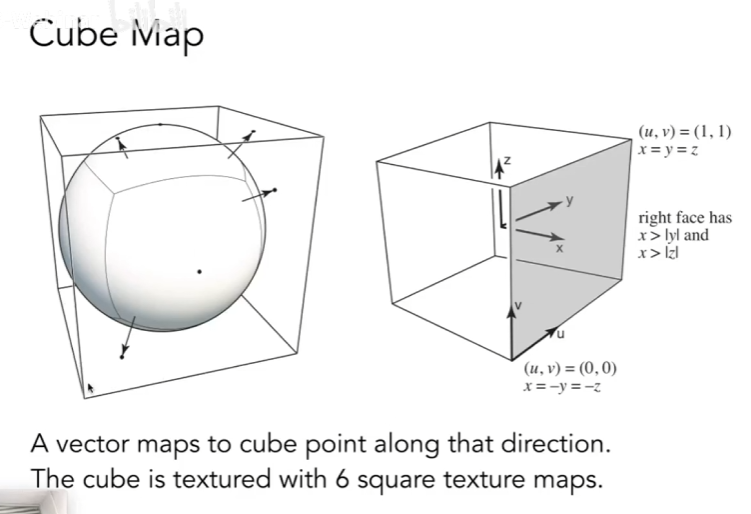
环境光映射 / 环境光贴图 Environment Map

用纹理球描述环境光 Spherical Enviroment Map

问题：靠近极点会产生扭曲 - Cube Map

image-20240409231234338

凹凸贴图 / 法线贴图

纹理不一定只能用来表示颜色，我们可以用纹理来表示凹凸

这可以在不改变模型的情况下制造凹凸的视觉效果

image-20240409232251581

位移贴图 Displacement map 会真的改变顶点，但是要求模型足够细致

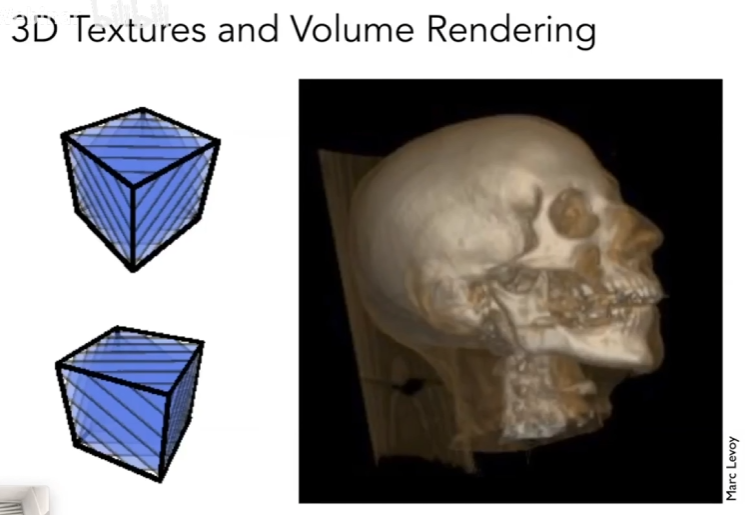
3D纹理

image-20240409232421871

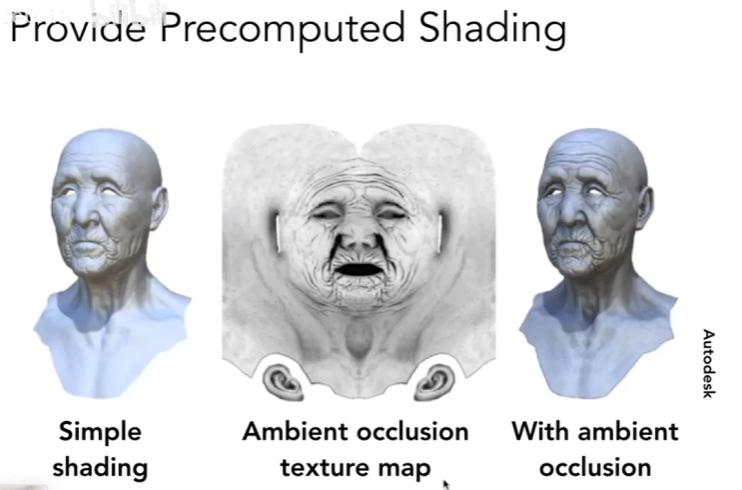
预计算着色

image-20240409232558384

体渲染

image-20240409232729220

Lecture 10 Geometry 1 (Introduction)

如何表示几何

隐式 Implicit

基于满足特定关系的点的集合

image-20240409233629874
  • 很难直观地描述几何形体，难以确定具体有哪些点在几何表面
  • 易于判定给定点与几何的相对位置关系，是否在几何内/外

显式 Explicit

所有点都直接显式给予或通过参数映射（uv）给予

image-20240409233958221

  • 易于进行直观地描述
  • 但难以判定点是否在几何内/外

几何表示法

直接通过算术方法表示 - Implicit

image-20240409234509657

构造实体集合 Constructive Solid Geometry - Implicit

通过定义简单的基本几何与基本运算组合出复杂几何

image-20240409234633507

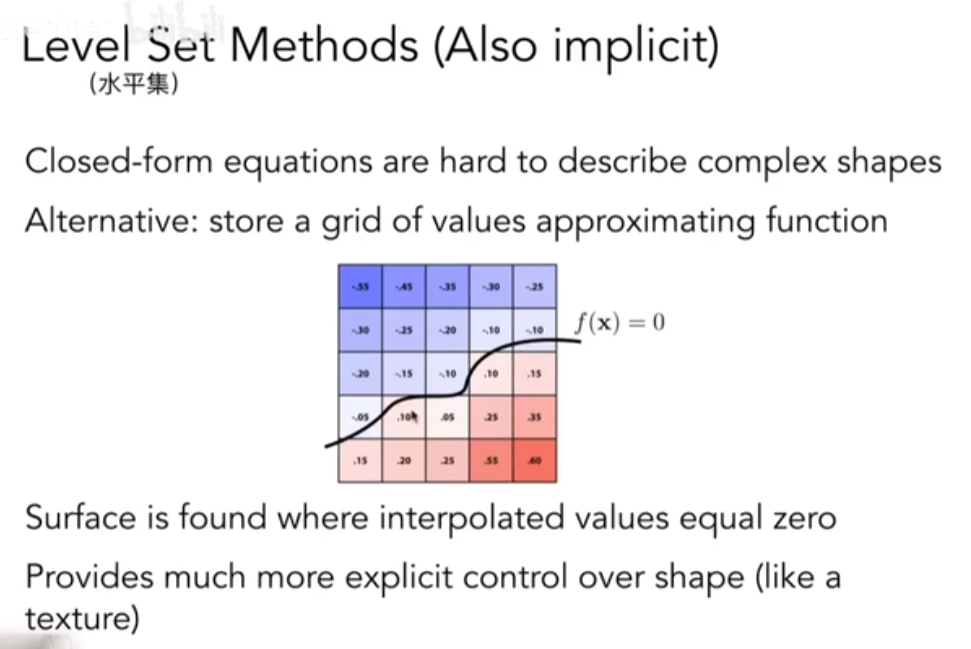
距离函数 Distance Functions - Implicit

定义距离函数来表示几何：用空间中的每个点到边界的最佳距离来描述几何 - SDF

image-20240409234744278 image-20240409234819893

任意两个距离函数都可以被很好地Blend

距离函数的表示能力非常强

image-20240409235257267

分形 - Implicit

image-20240409235412470

Lecture 11 Geometry 2 (Curves and Surfaces)

几何表示法

点云 Point Cloud - Explicit

最简单的显式表示法 - 一个点的列表

扫描直接得到的三维数据通常是点云

多边形面 Polygon Mesh - Explicit

最常用的形式

image-20240423222236050

.obj最直接的文件格式

image-20240423222321040

曲线 Curves

贝赛尔曲线

image-20240423222657426

De Casteljau Algorithm

image-20240423222928765 image-20240423223359167 image-20240423223938757
  • 仿射变换不变
  • 一定在凸包内

分段贝塞尔曲线 Piecewise

当贝塞尔曲线控制点过多时，容易出现曲线不明显且十分耗时的情况

可以通过分段求解贝塞尔曲线来解决这点

一般会采用每四个控制点一组，这有利于对曲线的控制

只要保证导数连续便可以保证贝塞尔曲线的光滑

其他曲线

Splines - 样条

image-20240423224901762

B-Splines

image-20240423224939546 image-20240423225058605

曲面 Surfaces

贝塞尔曲面

可以用贝塞尔曲线得到贝塞尔曲面

类似双线性插值

网格操作：几何处理

  • 网格细分 Mesh subdivision
  • 网格简化 Mesh simplification
  • 网格正规化 Mesh regularization

Lecture 12 Geometry 3

网格细分

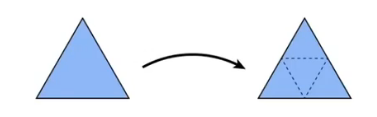
Loop Subdivision

  • 把每个三角形分为4个
image-20240424104823067
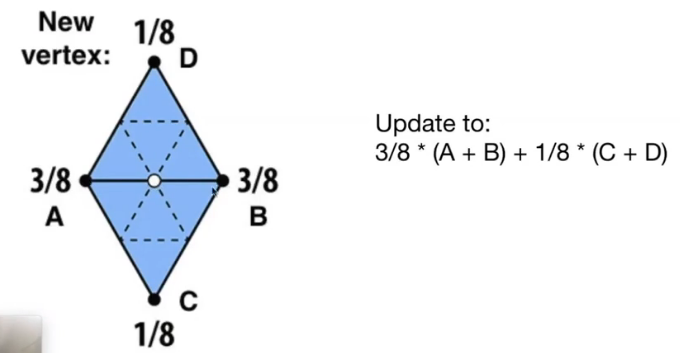
  • 根据权重分配新的顶点

对于新的顶点：

image-20240424104950516

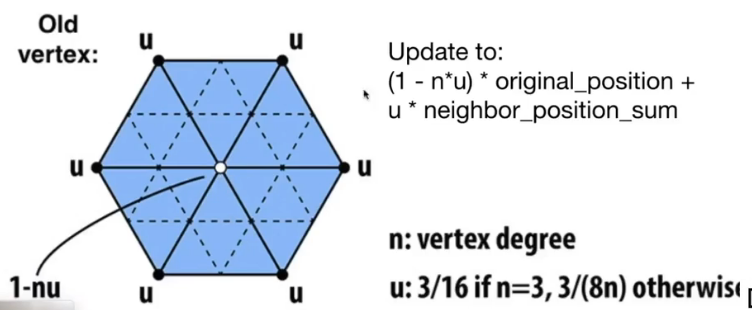
对于旧的顶点：

image-20240424105058537

Catmull-Clark Subdivision

Loop Subdiversion只能作用于全部由三角形构成的网格

而Catmull-Clark细分可以作用于所有的网格

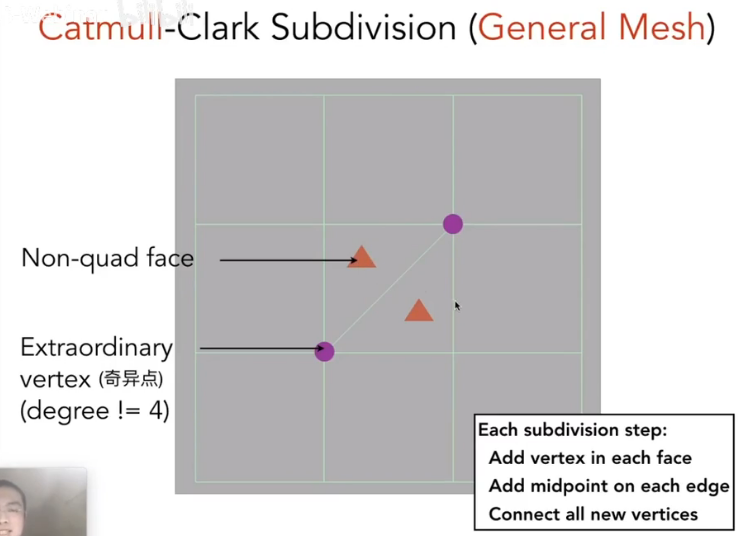
image-20240424110141944 image-20240424110527959

每个非四边形面在一次C-C细分后都会为增加一个奇异点，但一次细分之后，奇异点数量不再改变

image-20240424110807142

网格简化

目标：减少网格数量，但保持整体的形体

边坍缩 Collapsing An Edge

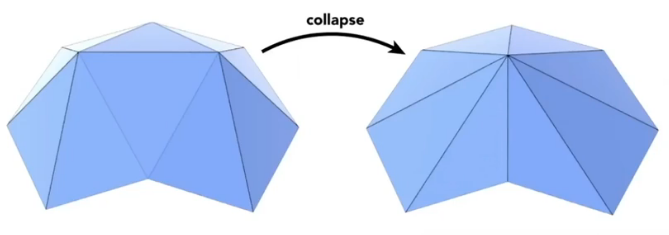
image-20240424111334348

二次误差度量 Quadric Error Metrics

决定边坍缩的目标

image-20240424111520623

通过二次度量误差进行简化

让最终点到其他点的距离的平方和最小

对模型中的每条边，假设其被坍缩，计算其探索后的最佳点的二次度量误差值，最后取所有边中误差值最小的边进行探索

使用优先队列/堆

image-20240424111924542 image-20240424112001065

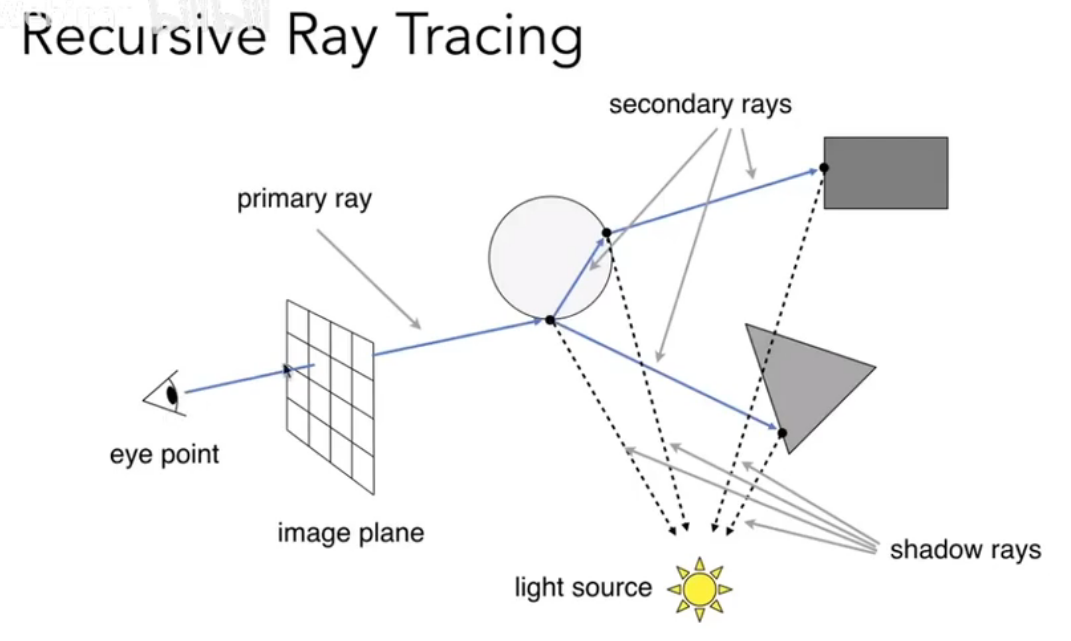
阴影映射 Shadow Mapping

  • 一种图像空间算法
  • 可能会产生走样
  • Key Idea: 不在阴影里的点一定同时被光源和摄像机照到

Shadow Mapping只能应用于点光源

PASS:

  1. Render from Light
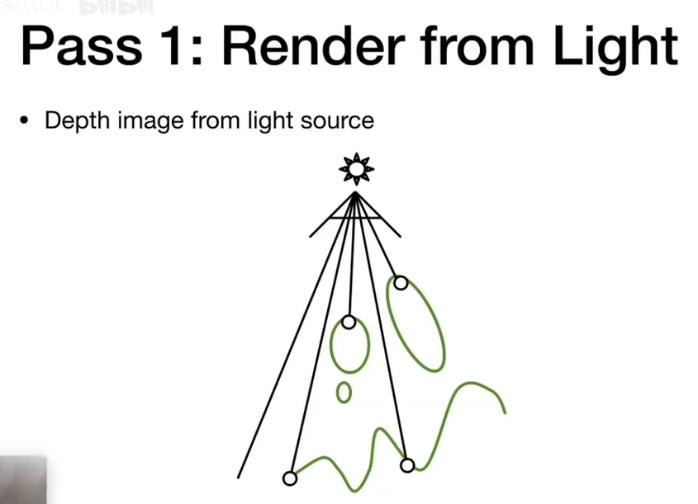
image-20240424112754130

得到光源视角的深度图

  1. Render from Eye
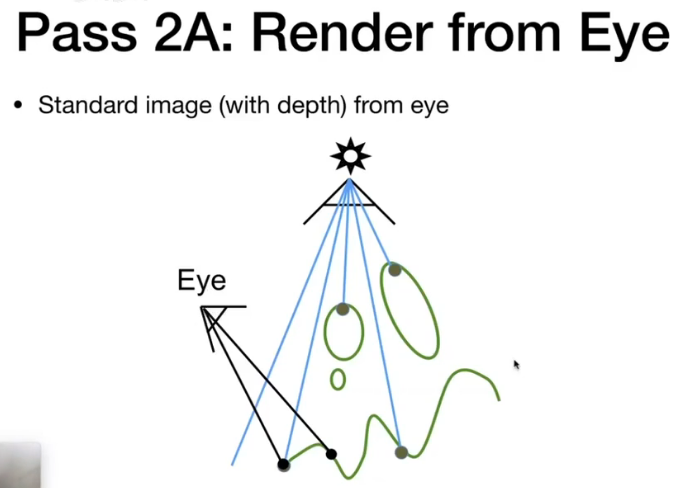
image-20240424112929974

得到相机视角的标准图（带深度）

  1. Project to Light
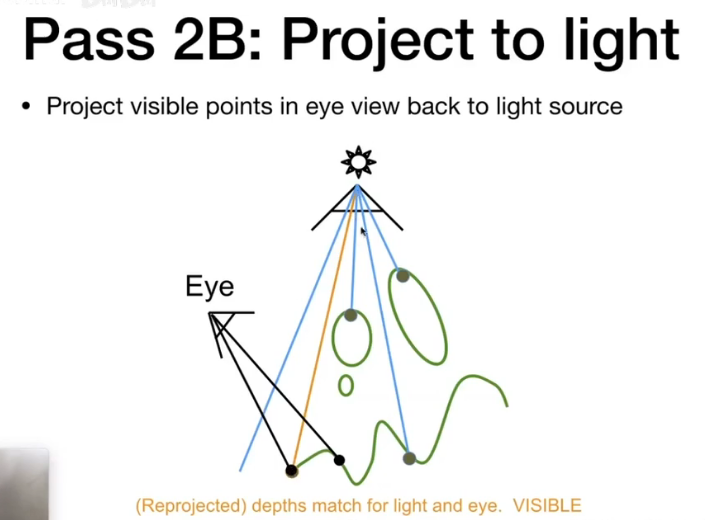
image-20240424113009525

将相机视角看到的点投影回光源

比较二者的深度，如果深度相同则在阴影外；反之则在阴影内

硬阴影与软阴影

image-20240424114158623

Lecture 13 Ray Tracing 1 (Whitted-Style Ray Tracing)

Why Ray Tracing?

  • 光栅化在处理全局效果时并不好
image-20240507204933189
  • 光栅化很快，但是质量却不太好
  • 光线追踪很准确，但是很慢

光线

  • 光线沿直线传播
  • 光线之间不会相互影响
  • 光线从光源出发最后到达我们的眼睛（光线是可逆的）

光线投射

image-20240507212453824

Whitted-Style Ray Tracing

image-20240507212405482

任一点的光线可以继续传播（反射、折射）

对每一个弹射点计算其着色，最后一起加到原先的像素点上

image-20240507213021646

求交点

对于隐式几何：求方程组的解即可

对于显式几何：

image-20240514230719291

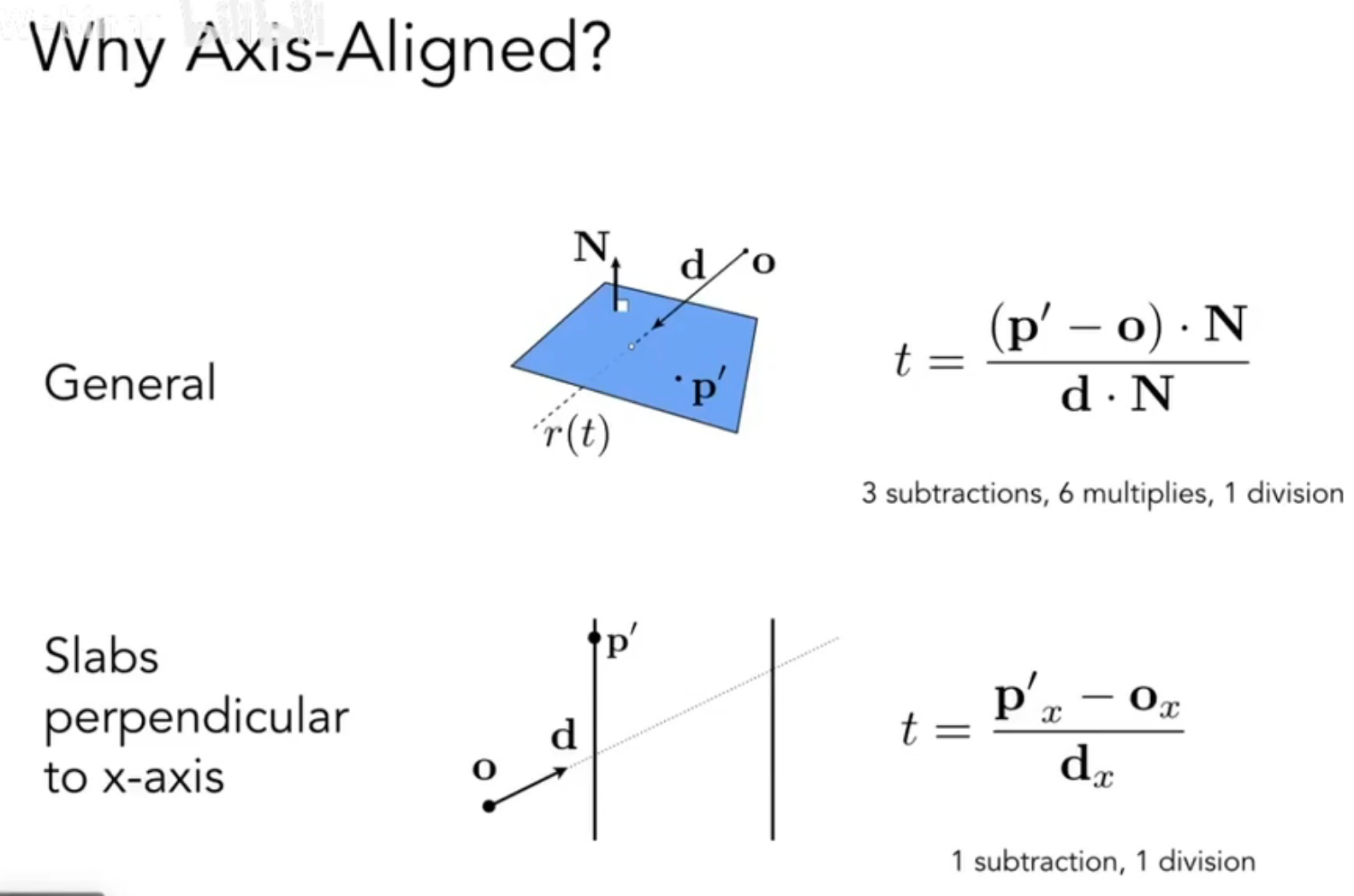
点与平面求交：

image-20240514230933593 image-20240514231002061

MT算法：重心坐标求点是否在三角形内

image-20240507221808203

加速求交

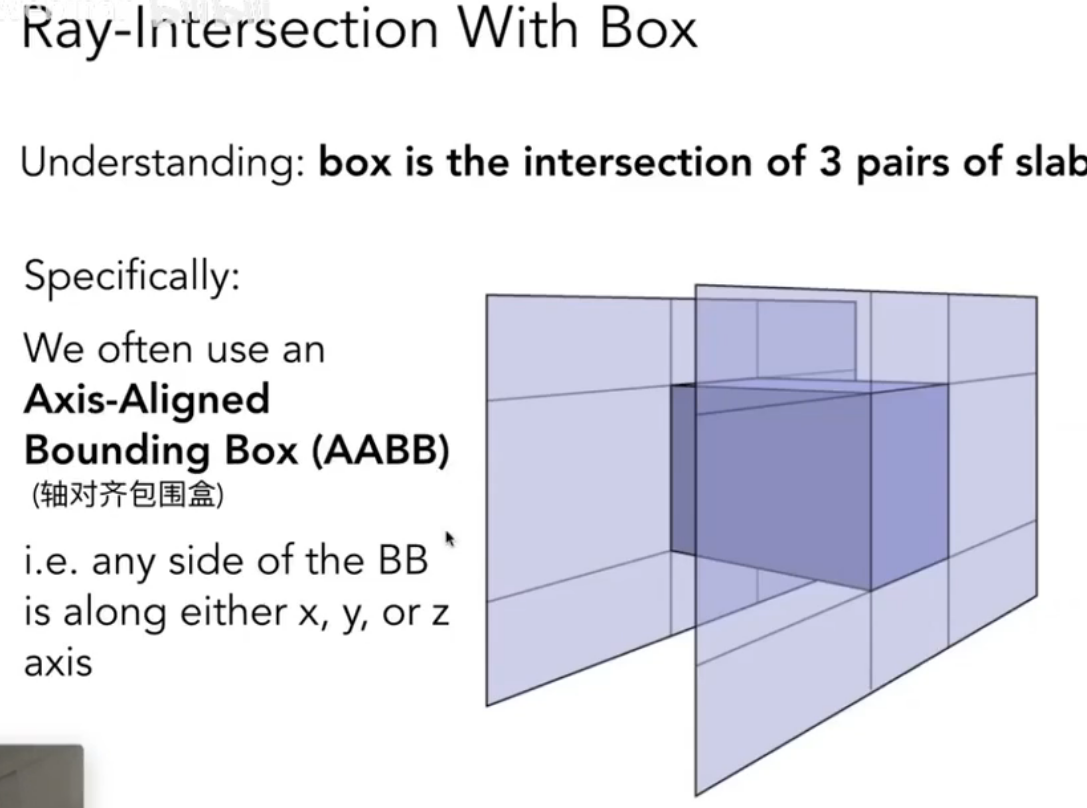
包围盒 / 包围体积

image-20240507222603012

长方体：空间中三个对面的交集

AABB-轴对齐包围盒

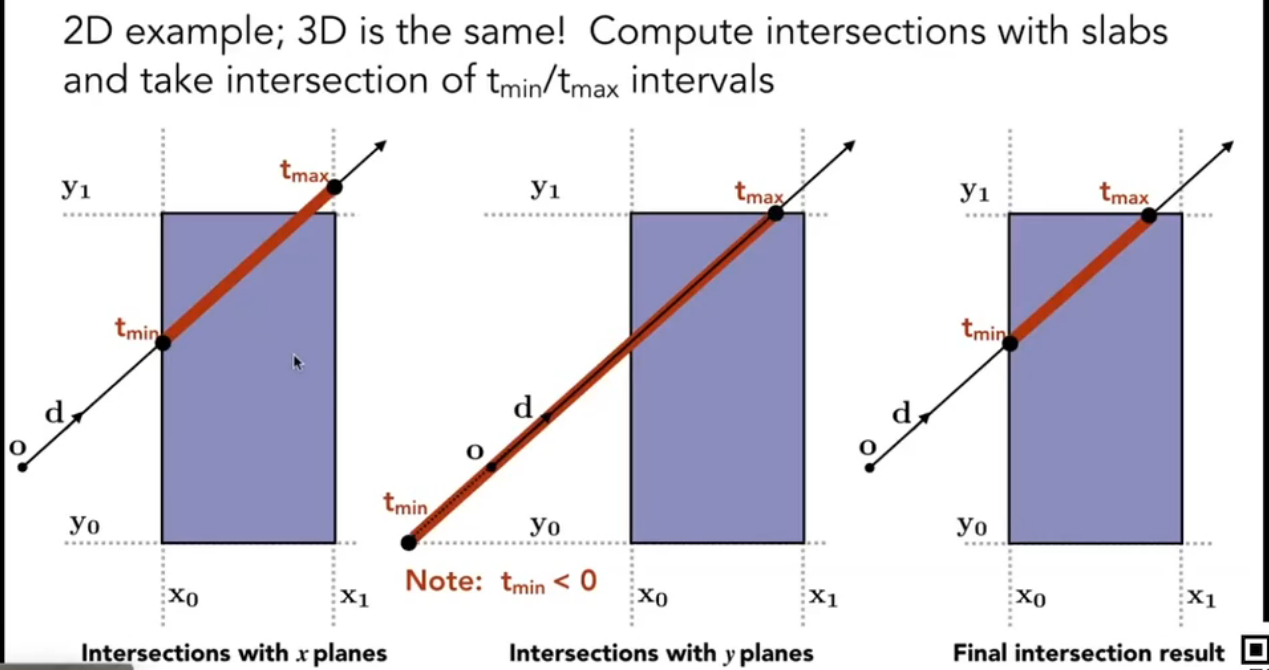
image-20240507222836202 image-20240507223617046 image-20240507223830054
  • 如果texit<0t_{exit}<0 - 盒子在射线之后，没有交点
  • 如果texit>=0t_{exit}>=0且tenter<0t_{enter}<0 - 射线起点在盒子内部，一定有交点

tenter<texit且texit>=0t_{enter}<t_{exit}且t_{exit}>=0

image-20240507224554035

Lecture 14 Ray Tracing 2 (Acceleration & Radiometry)

使用AABBs（轴对齐包围盒）加速光追

Uniform grids

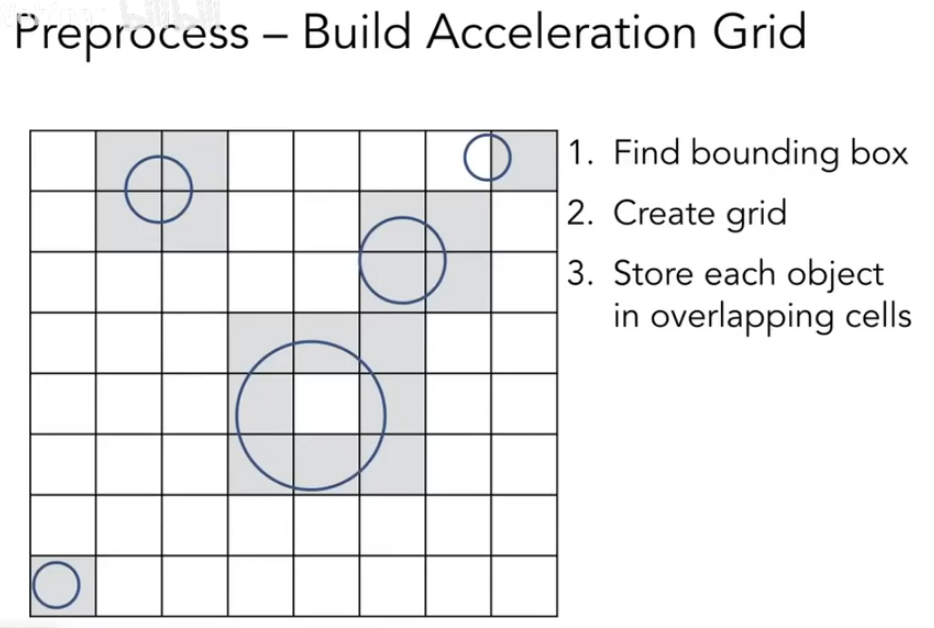
image-20240514232118267 image-20240514232222213
  1. 找到包围盒
  2. 创建格子
  3. 标记有东西的盒子

多做和盒子的求交，少做和物体的求交

格子的密度需要平衡

image-20240514232412971

物体分布越均匀越适合使用Uniform Grids

Spatial partitions - 空间划分

image-20240514232623799

  • Oct-Tree 八叉树：在维度升高后划分数量会几何级增加，不适合处理高维坐标

  • KD-Tree：和八叉树原理基本相同，但是其划分不会受到维度影响，每次只切一刀；横竖交替划分，使得划分更加均匀

  • BSP-Tree：和KD-Tree很想，但划分不是延轴的

image-20240514233253563 image-20240514233316280

KD-Tree的问题：

  • 包围盒和三角形是否有交点的计算十分复杂
  • 一个物体可能出现在多个叶子结点中

Object partitions & Bounding Volume Hierarch (BVH)

最常用，很大程度上解决了KD-Tree的问题

BVH不划分空间，而是划分物体

先分物体，再求包围盒

  • 优点：一个物体只可能出现在一个叶子结点
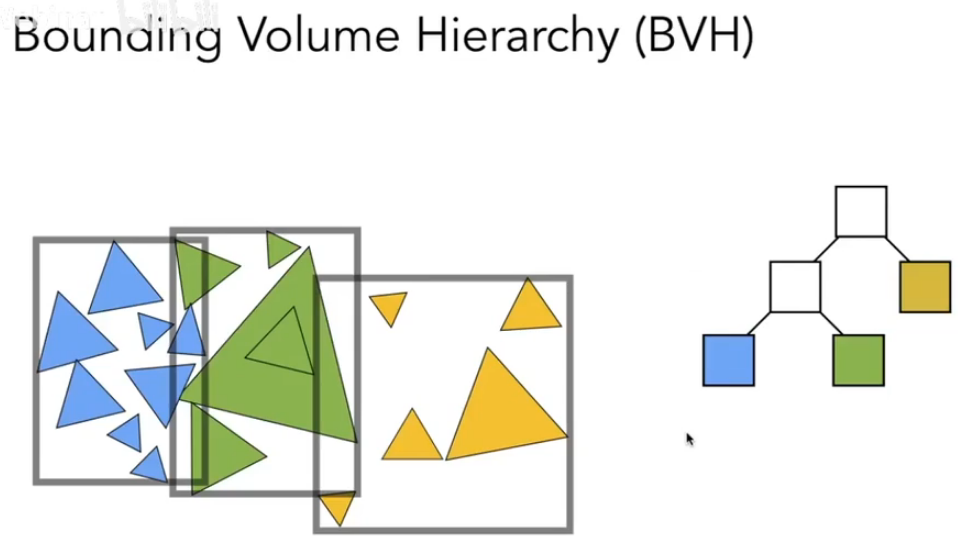
image-20240514234327580
  • 缺点：BVH划分的出的区块有可能重叠
image-20240514234546284 image-20240514235045913

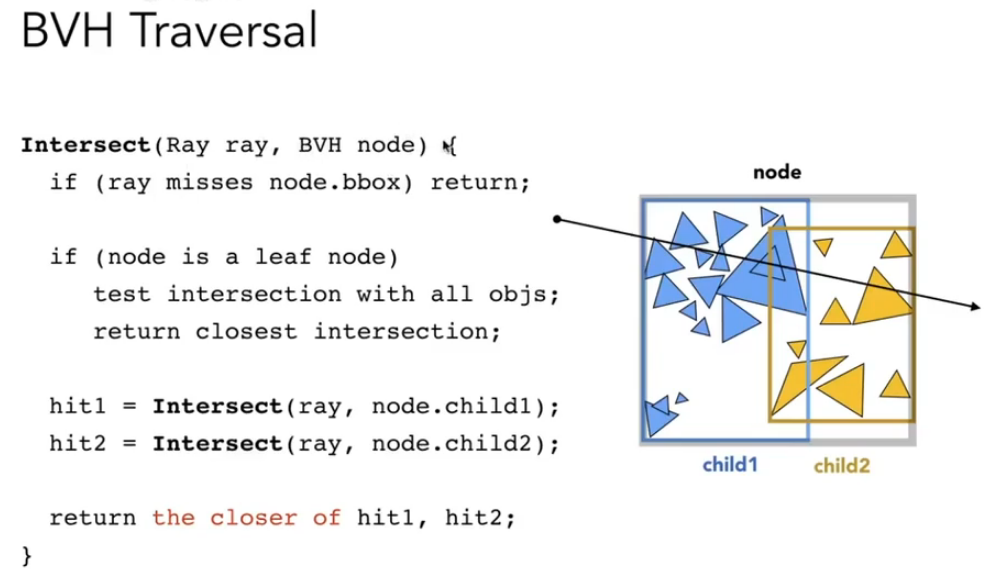
BVH算法伪代码：

image-20240514235130386 image-20240514235235220

Basic Radiometry - 辐射度量学

在之前的着色与反射模型中，我们常常通过经验来定义公式，这是可行的，也可以得到很好的效果。但经验始终只是经验，辐射度量学可以给出基于物理的准确定义光照的方法

  • 描述光照的单位与体系
  • 基于空间光学
  • Radiant Flux 辐射通量 - Intensity 辐射强度 - Irradiance 辐照度 - Radiance 辐亮度

Radient Energy and Flux(Power)

image-20240515091324405

流明 lm - 功率 W

image-20240515092941308

Flux另一种理解：单位时间内通过某一平面的光子量

光的度量

image-20240515093116778

Radiant Intensity

image-20240515093209773

单位立体角发出的能量 - Wsr=lmsr=cd=candela\frac{W}{sr}=\frac{lm}{sr}=cd=candela​

立体角
image-20240515094958876 image-20240515095316837
Intensity
image-20240515095519264 image-20240515095702532

Irradiance

Radiance