官网：https://algs4.cs.princeton.edu/home/
笔记目录：https://hmxs.games/posts/25550/

排序

排序就是将一组对象按照某种逻辑顺序重新排列的过程，其在商业数据处理和现代科学计算方面都有着重要的地位，本章将聚焦于排序算法，介绍、研究并实现几种经典的排序算法。

前言

排序算法模板

在实现排序算法时，我们将会遵照一定的“游戏规则”，以下SortExample展示了我们对于排序算法的约定

public class SortExample
{
    public static void sort(Comparable[] a){ }

    private static boolean less(Comparable v, Comparable w)
    { return v.compareTo(w) < 0; }

    private static void exchange(Comparable[] a, int i, int j)
    { Comparable t = a[i]; a[i] = a[j]; a[j] = t; }

    private static void show(Comparable[] a)
    {
        for (int i = 0; i < a.length; i++)
            System.out.print(a[i] + " ");
        System.out.println();
    }

    public static boolean isSorted(Comparable[] a)
    {
        for (int i = 1; i < a.length; i++)
            if (less(a[i], a[i-1])) return false;
        return true;
    }

    public static void main(String[] args)
    {
        String[] a = In.readStrings();

        sort(a);
        assert isSorted(a);
        show(a);
    }
}

sort：排序的具体实现
less：比较两个数据的大小
exchange：交换两个数据
show：打印数组
isSorted：检查是否成功排序

性能评估

排序成本模型：在研究排序算法时，我们需要计算比较和交换的数量。对于不交换元素的算法，我们会计算访问数组的次数

算法比较

当我们实现了好几种排序算法后，我们自然想知道他们哪个更快，而以下的SortCompare类便可以帮助我们实现这点

public class SortCompare
{
    public static double time(String alg, Double[] a)
    {
        Stopwatch timer = new Stopwatch();

        if (alg.equals("Insertion")) InsertionSort.sort(a);
        if (alg.equals("Selection")) SelectionSort.sort(a);

        return timer.elapsedTime();
    }

    public static double timeRandomInput(String alg, int N, int T)
    {
        double total = 0.0;
        Double[] a = new Double[N];
        for (int t = 0; t < T; t++)
        {
            for (int i = 0; i < N; i++)
                a[i] = Math.random();
            total += time(alg, a);
        }
        return total;
    }

    public static void main(String[] args)
    {
        String alg1 = args[0];
        String alg2 = args[1];
        int N = Integer.parseInt(args[2]); // array size
        int T = Integer.parseInt(args[3]); // number of trials
        double t1 = timeRandomInput(alg1, N, T); // total for alg1
        double t2 = timeRandomInput(alg2, N, T); // total for alg2
        System.out.printf("For %d random Doubles\n    %s is", N, alg1);
        System.out.printf(" %.1f times faster than %s\n", t2/t1, alg2);
    }
}

这里以马上要实现的选择排序与插入排序的比较为例，实现了跟多排序算法后，在time()中添加即可

上面的排序算法以完全随机生成的数组作为排序算法的输入，通过多次实验保证实验结果的有效性，并且我们通过改变输入改变输入的规模以进行更精确的测试

选择排序

这是最简单的排序算法之一，其核心思想是：不断选择最小/大的元素

我们会先找到数组中最小/大的元素，将其与数组的第一个元素交换位置；之后，在剩下的元素中找到最小/大的元素，将其与第二个元素交换位置；之后不断重复这一过程，直至最后一个元素

实现

public static void sort(Comparable[] a)
{
    int N = a.length;
    for (int i = 0; i < N; i++)
    {
        int min = i;
        for (int j = i + 1; j < N; j++)
            if (less(a[j], a[min]))
                min = j;
        if (min != i)
            exchange(a, i, min);
    }
}

分析

对于长度为 $N$ 的数组，选择排序需要大约 $N^2/2$ 此比较与 $N$ 次比较，其时间复杂度为 $N^2$ 级别

其有两个鲜明的特点：

运行时间与输入无关：无论输入数组排序状态如何，是有序还是无序，对选择排序的运行效率都没有影响
数据移动时最少的：选择排序的交换次数与数组大小是线性关系，其余任何算法都不具备这个特性（大部分都是 $Nlg N$ 或 $N^2$ 级别）

插入排序

插入排序的核心思想就如同在斗地主时整理手牌：将每张牌插入到已有的有序牌中的适当位置

在算法的实现中，由于要给元素腾出位置，我们需要将其余元素向右移动一位；与选择排序相同，索引左边的元素都是有序的，而当索引到达数组右端时，排序便完成了

实现

public static void sort(Comparable[] a)
{
    int N = a.length;
    for (int i = 1; i < N; i++)
        for (int j = i; j > 0 && less(a[j], a[j-1]); j--)
            exchange(a, j, j-1);
}

分析

对于长度为 $N$ 的数组选择排序，其时间复杂度为 $N^2$ 级别

插入排序在部分情况下非常有效，其实际效率很大程度上取决于其需要进行插入的次数

如果数组中倒置的数量小于数组大小的某个倍数，那么我们说这个数组是部分有序的。下面是几种典型的部分有序的数组：

数组中每个元素距离它的最终位置都不远
一个有序的大数组接一个小数组
数组中只有几个元素的位置不正确

插入排序对这样的数组很有效，而选择排序则不然；事实上，当倒置数量很少时，插入排序很可能比其他任何算法都快

希尔排序

希尔排序是一种基于插入排序的排序算法，其核心思想是：交换不相邻的元素以对数组的局部进行排序，并最终用插入排序将局部有序的数组排序

在上面对于插入排序的分析中，我们了解到：当数组是部分有序的时，插入排序非常快；而希尔排序正是利用了这点，先使数组变得部分有序，再进行进一步的排序，以加快插入排序的速度

如下图所示，希尔排序会以h为步长将数组进行分割，假设数组为[5, 7, 1, 4, 6, 9]，且 $h=3$ ，则数组会被分割为[5, 4]、[7, 6]、[1, 9]三组；首先对组内进行插入排序（一个更简单的方法是在子数组中将每个元素交换到比它大的元素之前去即可），便可以得到[4, 5]、[6, 7]、[1, 9]，这被称为h有序数组；之后我们便可以进一步缩小h，以得到更大的h有序数组，最后实现数组的排序

我们也可以从这一角度去思考：如果 $h$ 较大，在进行组内排序时便可以将元素移动到很远的地方，而插入排序只能一个个的进行元素移动，从而提高效率

在我们下面的实现中，使用了序列 $1/2（3k-1)$ ，即从 $N/3$ 开始递减至 1。我们把这个序列称为递增序列；下面的实现中实时计算了其递增序列，另一种方式是将递增序列存储在一个数组中

实现

public static void sort(Comparable[] a)
{
    int N = a.length;
    int h = 1;
    while (h < N/3)
        h = 3 * h + 1;
    while (h >= 1)
    {
        for (int i = h; i < N; i++)
            for (int j = i; j >= h && less(a[j], a[j-h]); j-=h)
                exchange(a, j, j-h);
        h = h / 3;
    }
}

分析

通过SortCompare进行比较我们可以发现，希尔排序比插入排序快了非常多

希尔排序更高效的原因是它权衡了子数组的规模和有序性

希尔排序之初，各个子数组都很短，排序之后子数组都是部分有序的，这两种情况都很适合插入排序

而子数组部分有序的程度取决于递增序列的选择，但对于递增序列的选择是个复杂的问题：算法的性能不仅取决于 $h$ ，还取决于 $h$ 之间的数学性质，比如它们的公因子等；有很多论文研究了各种不同的递增序列，但都无法证明某个序列是“最好的”；在我们的实现中，使用了非常简单易于计算的底层序列，但一些复杂的序列可以被证明其性能好于我们使用的序列，更加优秀的递增序列有待我们去发现

透彻理解希尔排序的性能至今仍然是一项挑战；实际上，希尔排序是我们唯一无法准确描述其对于乱序的数组的性能特征的排序方法

归并排序

归并，即将两个有序数组合并成一个更大的有序数组；归并排序便是基于这一简单操作进行的

归并排序是一种基于分治思想的递归排序算法，要将一个数组排序，可以先（递归地）将它分成两半分别排序，然后将结果归并起来

归并排序的优点在于其能够保证，排序将任意长度为 $N$ 的数组所需的时间与 $NlogN$ 成正比；同时，其也存在所需的额外空间与 $N$ 成正比的缺点

归并的抽象实现

实现归并的一种直截了当的办法是将两个不同的有序数组归并到第三个数组中，创建一个适当大小的数组然后将两个输入数组中的元素一个个从小到大放入这个数组中即可

public static void merge(Comparable[] a, int low, int mid, int high)
{
    Comparable[] aux = new Comparable[a.length];
    for (int k = low; k <= high; k++)
        aux[k] = a[k];
    
    int i = low;
    int j = mid + 1;
    for (int k = low; k <= high; k++)
        if         (i > mid)				a[k] = aux[j++]; // 数组左半边已用尽
        else if (j > high)                a[k] = aux[i++]; // 数组右半边已用尽
        else if (less(aux[j], aux[i]))    a[k] = aux[j++]; // 右边的元素小
        else                            a[k] = aux[i++]; // 左边的元素小
}

以上的代码演示了进行一次归并时进行的操作，a是我们需要进行归并的数组，我们会先将a复制到aux辅助数组中，对左右两边的数组进行一一比较后，一个个放回a数组中完成排序

上述代码可以完成一次归并，但是当我们想要用归并将一个大数组排序时，我们便需要进行多次归并，上述的方法会在每进行一次归并时都对原数组进行一次完整的复制，这会带来大量的内存消耗

与此相比，我们更需要一种“原地归并”的方法，使得我们不需要用一个额外的数组来存储数据，但实际上这是较为困难且复杂的；不管怎么说，上述方法仍然是有意义的，其帮助我们对归并操作进行了抽象化，我们可以在此基础上继续探索

自顶向下的归并排序

基于归并的抽象实现，我们可以实现一种自顶向下的递归归并算法

这也是应用高效算法设计中分治思想的最典型的一个例子

实现

private static Comparable[] aux;

public static void sort(Comparable[] a)
{
    aux = new Comparable[a.length];
    sort(a, 0, a.length-1);
}

private static void sort(Comparable[] a, int low, int high)
{
    if (high <= low) return;
    int mid = low + (high - low) / 2;
    sort(a, low, mid);        // 对左半数组进行排序
    sort(a, mid+1, high);    // 对右半数组进行排序
    merge(a, low, mid, high);
}

private static void merge(Comparable[] a, int low, int mid, int high)
{
    // 将a[low..high]复制到aux[low..high]
    for (int k = low; k <= high; k++)
        aux[k] = a[k];

    int i = low, j = mid + 1;
    for (int k = low; k <= high; k++)
        if         (i > mid)               a[k] = aux[j++]; // 数组左半边已用尽
        else if (j > high)              a[k] = aux[i++]; // 数组右半边已用尽
        else if (less(aux[j], aux[i]))  a[k] = aux[j++]; // 右边的元素小
        else                            	a[k] = aux[i++]; // 左边的元素小
}

分析

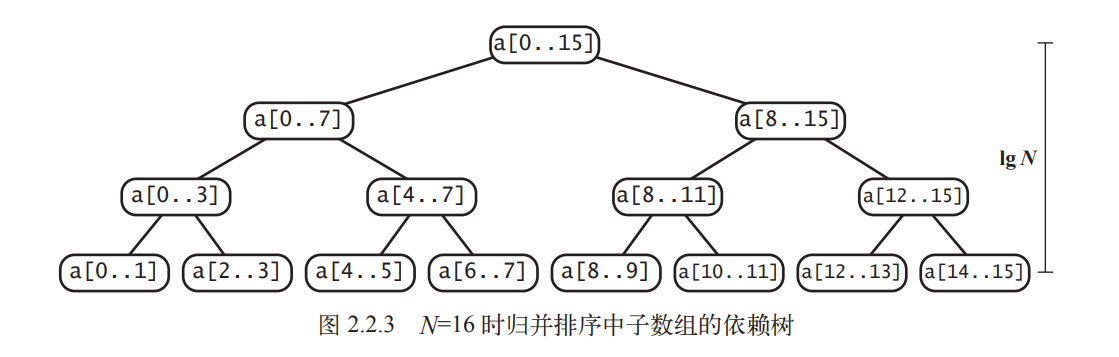
上图展示了自顶向下的归并排序算法的递归树

对于长度为 N 的任意数组，自顶向下的归并排序需要 $\frac{1}{2}NlgN$ 至 $NlgN$ 次比较；最多需要访问数组 $6NlgN$ 次

归并排序和之前的初级排序方法不可同日而语，它表明我们只需要比遍历整个数组多个对数因子的时间就能将一个庞大的数组排序；可以用归并排序处理数百万甚至更大规模的数组，这是插入排序或者选择排序做不到的

改进

通过一些细致的思考我们还能够大幅度缩短归并排序的运行时间：

对小规模子数组使用插入排序

递归会使小规模问题中方法的调用过于频繁，而在前面对于插入排序的研究中，我们可以发现插入排序对于小数组可能比归并排序更快；在分割数组到足够小后，我们便可以采用插入排序，之后再进行归并，这可以提高算法的效率

测试数组是否已经有序

我们可以添加一个判断条件，如果a[mid]小于等于a[mid+1]，我们就认为数组已经是有序的并跳过 merge() 方法。这个改动不影响排序的递归调用，但是任意有序的子数组算法的运行时间就变为线性的了

不将元素复制到辅助数组

我们可以节省将数组元素复制到用于归并的辅助数组所用的时间；这种方法需要一些技巧，我们要在递归调用的每个层次交换输入数组和辅助数组的角色；merge的过程类似对着一个源文本进行重新抄录，而此方法便是让两个数组轮流作为源文本

以下代码对上述三个优化进行了实现：

private static final int CUTOFF = 7; // 小数组的阈值，小数组应用插入排序

public static void sort(Comparable[] a)
{
    Comparable[] aux = a.clone();
    sort(aux, a, 0, a.length-1);
}

private static void sort(Comparable[] source, Comparable[] destination, int low, int high)
{
    if (high <= low + CUTOFF) // 优化：小数组应用插入排序
    {
        insertionSort(destination, low, high);
        return;
    }
    int mid = low + (high - low) / 2;
    sort(destination, source, low, mid); // 优化：交换source和destination的位置
    sort(destination, source, mid+1, high);
    if (!less(source[mid+1], source[mid])) // 优化：如果数组已经有序，就不需要归并了
    {
        System.arraycopy(source, low, destination, low, high - low + 1); // 复制数组
        return;
    }
    merge(source, destination, low, mid, high);
}

// source: 用于比较的数组，destination用于归并的目的地
private static void merge(Comparable[] source, Comparable[] destination, int low, int mid, int high)
{
    int i = low, j = mid + 1;
    for (int k = low; k <= high; k++)
        if (i > mid)         destination[k] = source[j++]; // 数组左半边已用尽
        else if (j > high)     destination[k] = source[i++]; // 数组右半边已用尽
        else if (less(source[j], source[i])) destination[k] = source[j++]; // 右边的元素小
        else                                 destination[k] = source[i++]; // 左边的元素小
}

private static void insertionSort(Comparable[] a, int low, int high)
{
    for (int i = low; i <= high; i++)
        for (int j = i; j > low && less(a[j], a[j-1]); j--)
            exchange(a, j, j-1);
}

自底向上的归并排序

递归实现的归并排序是算法设计中分治思想的典型应用：我们将一个大问题分割成小问题分别解决，然后用所有小问题的答案来解决整个大问题；尽管我们考虑的问题是归并两个大数组，实际上我们归并的数组大多数都非常小

在自顶向下的归并排序中，我们会先从大数组入手，一步步将大数组分割为小数组；而我们实际上还可以直接从小数组入手，即把每个元素想象成一个大小为1的数组，然后两两归并、四四归并、八八归并…直到归并完成；这种归并排序的实现方法被称为自底向上的归并排序

实现

private static Comparable[] aux;

public static void sort(Comparable[] a)
{
    int N = a.length;
    aux = new Comparable[N];
    for (int sz = 1; sz < N; sz *= 2) // sz子数组大小
        for (int low = 0; low < N - sz; low += 2 * sz) // low: 子数组索引
            merge(a, low, low + sz - 1, Math.min(low + 2 * sz - 1, N - 1));
}

private static void merge(Comparable[] a, int low, int mid, int high)
{
    // 将a[low..high]复制到aux[low..high]
    for (int k = low; k <= high; k++)
        aux[k] = a[k];

    int i = low, j = mid + 1;
    for (int k = low; k <= high; k++)
    {
        if      (i > mid)               a[k] = aux[j++]; // 数组左半边已用尽
        else if (j > high)              a[k] = aux[i++]; // 数组右半边已用尽
        else if (less(aux[j], aux[i]))  a[k] = aux[j++]; // 右边的元素小
        else                            a[k] = aux[i++]; // 左边的元素小
    }
}

分析

对于长度为 $N$ 的任意数组，自底向上的归并排序需要 $\frac{1}{2}NlgN$ 至 $NlgN$ 次比较，最多访问数组 $6NlgN$ 次

这种实现方法的一个优势在于其比标准递归方法所需要的代码量要少很多

**当数组长度为2的幂时，自顶向下和自底向上的归并排序所用的比较次数和数组访问次数正好相同，只是顺序不同；**其他时候，两种方法的比较和数组访问的次序会有所不同

自底向上的归并排序比较适合用链表组织的数据，其只需要重新组织链表链接就能将链表原地排序，而不需要创建任何新的链表结点

用自顶向下或是自底向上的方式实现任何分治类的算法都很自然

排序算法的复杂度

学习归并排序的一个重要原因是它是证明计算复杂性领域的一个重要结论的基础

对于基于比较（Comparable）的排序算法来说，其具有以下性质（此处，我们忽略了访问数组的开销）

没有任何基于比较的算法能够保证使用少于 $lg(N!)～NlgN$ 次比较将长度为 $N$ 的数组排序

书中对于这一结论通过一个基于二叉树的数学模型给出了精彩的证明，这里不再赘述

这一性质告诉了我们在设计排序算法时能达到的上限与目标，如果没有这一结论，我们便可能会去尝试设计一个个在最坏情况下比较次数只有归并排序的一半的基于比较的算法；通过这一结论，我们便可以明确知道，这样的算法不存在

在上面对于归并排序的分析中，我们得到了归并排序在最坏情况下的比较次数为 $NlgN$ 这一结论，而在上面我们同样知道了没有任何排序算法能够用少于 $lg(N!)～NlgN$ 次比较将数组排序，这也就意味着：

归并排序是一种渐进最优的基于比较排序的算法

从严谨的角度来说，我们认为仅仅只需要 $lgN!$ 次比较的算法才是最优的排序算法，但在实际应用中，即使对于很大的 $N$ ，这种算法与归并排序之间的差异也并不明显

虽说我们已经盖棺定论地说归并排序已经是渐进最优了，但其仍然是有很多局限性的：

归并排序的空间复杂度不是最优的
在实践中不一定会遇到最坏情况
除了比较，算法的其他操作（例如访问数组）也可能很重要
不进行比较也能将某些数据排序

快速排序

终于来到大名鼎鼎的快速排序了，其可能是应用最为广泛的排序算法；快速排序实现简单、对输入的抵赖低同时在一般应用中比其他排序算法都要快得多，其在内存与效率上都非常优秀

内存上，快速排序是原地排序，其只需要一个很小的辅助栈
效率上，快速排序将长度为 $N$ 的数组排序所需的时间和 $NlgN$ 成正比。

基本实现

快速排序同归并排序一样，也是一种基于分治思想的递归排序算法，它们都会将数组进行分割，并分别排序，不同的是它们在实现思路上是相反的，或者说互补的：

归并排序会先对数组进行分割，然后将分割完成的数组分别排序，最后将已经有序的子数组进行归并从而实现对整个数组的排序；总的来说，归并排序是先递归再处理数组
快速排序的思想则是其会依据数组元素的大小对数组进行分割，即“是当两个子数组都有序时整个数组也就自然有序了”；其是先处理数组再进行递归的

形象的说，归并是在递归到底层之后向上返回的过程中完成对数组的排序；而快排则是当递归到底层后，排序就已经完成了

相对应的，归并排序中会通过递归调用“归并（merge）”来排序数组，而快速排序则是通过“切分（partition）”

当我们对一个数组进行切分时，我们会从其中选定一个“切分元素”，之后通过元素交换实现：切分元素左边的元素都小于它，而其右边的元素都大于它

通过递归地对数组进行切分，我们便可以完成对数组的排序，这便是快速排序的基本原理，下面便可以开始实现了

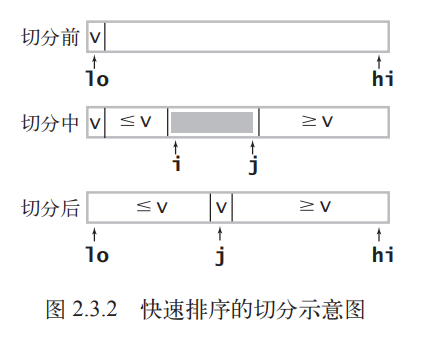
如上图所示，要实现快速排序的切分，一般的策略是先随意取一个元素作为切分元素，这里先取a[lo]，即最左边的元素；然后我们从数组的左端开始使用指针i向右扫描直到找到一个大于等于它的元素，再从数组的右端开始使用指针j向左扫描直到找到一个小于等于它的元素；这两个元素显然是没有排定的，因此我们交换它们的位置；如此继续，直到i与j相遇，再将切分元素交换到中间，我们就可以实现切分效果了

以下快速排序的基本实现：

public static void sort(Comparable[] a)
{
    StdRandom.shuffle(a);
    sort(a, 0, a.length-1);
}

private static void sort(Comparable[] a, int low, int high)
{
    if (high <= low) return;
    int j = partition(a, low, high);
    sort(a, low, j-1); // 将左半部分a[low..j-1]排序
    sort(a, j+1, high); // 将右半部分a[j+1..high]排序
}

private static int partition(Comparable[] a, int low, int high)
{
    int i = low, j = high + 1; // 左右扫描指针
    Comparable v = a[low]; // 切分元素
    while (true)
    {
        // 扫描左右，检查扫描是否结束并交换元素
        while (less(a[++i], v)) if (i == high) break;
        while (less(v, a[--j])) if (low == j) break;
        if (i >= j) break;
        exchange(a, i, j);
    }
    exchange(a, j, low); // 将v = a[j]放入正确的位置
    return j;
}

避免糟糕的实现

快速排序有着无数优点，但其非常“脆弱”，一些糟糕的实现会很容易导致糟糕的性能，让快速排序变成超慢排序🤣

以下是一些要点：

原地切分

我们可以轻易地像实现归并排序那样用一个辅助数组来实现切分，但其中因为开辟数组与数组复制所带来的的内存与效率损失会让我得不偿失

数组越界问题

在切分的内循环中，我们会依据切分元素扫描数组，而当切分元素是最小或最大的元素时，数组越界的问题便可能发生，在我们上面的实现中，我们通过if (i == high) break与if (low == j) break预防了这个问题

但实际上，上面实现中的if (low == j) break存在冗余，因为我们选择的切分元素是数组最左边的元素，而实际上a[j]无论如何也不会小于a[low]，所以这条语句实际上是可以删去的，在这一情况下，切分元素本身被作为了“哨兵”，防止了数组越界的产生

而实际上，我们也可以手动在数组最右端制造一个“哨兵”，如此一来if (i == high) break便也可以省去了；我们可以在开始排序前，将最大的元素放置在数组最右边，同时在递归左半部分的数组时，将上一轮的切分元素包含，即由sort(a, low, j-1)变为sort(a, low, j)，因为上一轮的切分元素一定大于其左边的所有元素；这样在所有切分中，最右端的元素都是最大的，可以起到“哨兵”的作用了

打乱数组，保持随机

我们可以注意到，在排序开始前，我们使用StdRandom.shuffle(a)对数组进行了打乱，这一来是对算法效率测试的保证；二来，快速排序在面对一些特殊输入时会有极差的性能，如我们每次选取的切分元素都是最大/最小的元素，效率会来到 $N^2$ 级别，打乱数组可以避免这一点

循环终止条件

正确地检测指针是否越界需要一点技巧，并不像看上去那么容易；一个最常见的错误是没有考虑到数组中可能包含和切分元素的值相同的其他元素

处理切分元素值有重复的情况

左侧扫描最好是在遇到大于等于切分元素值的元素时停下，右侧扫描则是遇到小于等于切分元素值的元素时停下；尽管这样可能会不必要地将一些等值的元素交换，但在某些典型应用中，它能够避免算法的运行时间变为平方级别；稍后我们会讨论另一种可以更好地处理含有大量重复值的数组的方法

递归终止条件

实现快速排序时一个常见的错误就是不能保证将切分元素放入正确的位置，从而导致程序在切分元素正好是子数组的最大或是最小元素时陷入了无限的递归循环之中

分析

快速排序的效率如此之高的一个很重要的原因得益于其简洁高效的切分内循环，在快速排序的切分方法中环会用一个递增的索引将数组元素和一个定值比较，而希尔排序与归并排序则还需要在内循环中进行数据的移动

快速排序另一个速度优势在于它的比较次数很少

将长度为 N 的无重复数组排序，快速排序平均需要 $~2NlnN$ 次比较（以及 $\frac{1}{6}$ 的交换）

总的来说，可以肯定的是对于大小为 $N$ 的数组，快速排序的运行时间在 $1.39NlgN$ 的某个常数因子的范围之内；归并排序也能做到这一点，但是快速排序一般会更快（尽管它的比较次数多 $39\%$ ），因为它移动数据的次数更少；这些保证都来自于数学概率

改进

快速排序是由 C.A.R Hoare 在 1960 年发明的，几乎从 Hoare 第一次发表这个算法开始，人们就不断地提出各种改进方法；并不是所有的想法都可行，因为快速排序的平衡性已经非常好，改进所带来的提高可能会被意外的副作用所抵消；但其中一些，也是我们现在要介绍的，非常有效

对小规模子数组使用插入排序

同样的方法我们在之前介绍归并排序的改进方法时已经用过，此处的思路也差不多

对于小数组，快速排序比插入排序慢
因为递归，快速排序的sort()方法在小数组中也会调用自己

我们只需要将if (high <= low) return;替换为if (high <= low + M) { Insertion.sort(a, lo, hi); return; }即可

切换阈值M的最佳值是和系统相关的，但是5～15之间的任意值在大多数情况下都能令人满意

三取样切分

快速排序的效率很大程度上取决于切分元素的选择，其最优情况便是切分元素正好等于数组元素的中位数，但要计算出这一数值便意味着我们需要在每次切分时都进行一次遍历，这是得不偿失的

在我们目前的实现中，我们通过打乱数组完全消除了输入的影响，使得切分元素的选取完全随机，这样可以在完全不计算中位数的情况下达到平均的效率

而取样切分则使用子数组的一小部分元素的中位数来切分数组，这可以让切分更优秀，虽然同样会付出计算中位数的代价，但这明显比遍历好多了，这种代价是可以接受的；人们发现将取样大小设为3并用大小居中的元素切分的效果最好

同时，取样切分可以带来的额外好处是，我们不需要进行特别的处理便可以将取样元素所谓哨兵使用，这样可以去除切分算法中的边界检查

private static int partition(Comparable[] a, int low, int high)
{
    // 三取样切分
    int mid = (low + high) / 2;
    if (less(a[mid], a[low])) exchange(a, low, mid);
    if (less(a[high], a[low])) exchange(a, low, high);
    if (less(a[high], a[mid])) exchange(a, mid, high);

    Comparable v = a[mid]; // 切分元素: a[low] <= a[mid] <= a[high]

    int i = low, j = high + 1; // 左右扫描指针
    while (true)
    {
        // 扫描左右，检查扫描是否结束并交换元素
        while (less(a[++i], v));
        while (less(v, a[--j]));
        if (i >= j) break;
        exchange(a, i, j);
    }
    exchange(a, j, low); // 将v = a[j]放入正确的位置
    return j;
}